課程內容:
《完全平方公式》
探究:計算下列各式,你能發現什么規律?
(1)(p+1)2=(p+1)(p+1)=_____________
(2)(m+2)2=_______________;
(3)(p-1)2=(p-1)(p-1)=__________________;
(4)(m-2)2=________________。
一般地,我們有(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2
即兩數和(或差)的平方,等于它們的平方和,加(或減)它們的積的2倍。這兩個公式叫做(乘法的)完全平方公式。
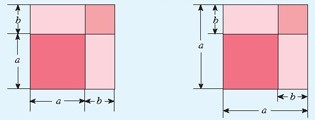
討論:你能根據下圖中的面積說明完全平方公式嗎?
例1:運用完全平方公式計算:
(1)(4m+n)2; (2)(y-1/2)2
例2:運用完全平方公式計算:
(1)1022; (2)992
思考:(a+b)2與(-a-b)2相等嗎?(a-b)2與(b-a)2相等嗎?(a-b)2與a2-b2相等嗎?為什么?
練習:
1.運用完全平方公式計算:
(1)(x+6)2;(2)(y-5)2;(3)(-2x+5)2;(4)
2.下面各式的計算錯在哪里?應當怎樣改正?
(1)(a+b)2=a2+b2;(2)(a-b)2=a2-b2。
歸納:添括號時,如果括號前面是正號,括到括號里的各項都不變號;如果括號前面是負號,括到括號里的各項都改變符號。
例3.運用乘法公式計算。
(1)(x+2y-3)(x-2y+3);(2)(a+b+c)2。
練習:
1.在等號右邊的括號內填上適當的項:
(1)a+b+c=a+( );(2)a-b-c=a-( )
(3)a-b+c=a-( );(4)a+b+c=a-( )
2.運用乘法公式計算:
(1)(a+2b-1)2;(2)(2x+y+z)(2x-y-z)
3.如圖,一塊直徑為a+b的圓形鋼板,從中挖去直徑分別為a與b的兩個圓,求剩下的鋼板的面積。
此內容正在抓緊時間編輯中,請耐心等待
尚老師
男,中教高級職稱
長期從事中學數學教學工作,重視學生對知識的理解與運用,市優秀教師、骨干教師,數學學科帶頭人。
























