課程內容
《平行線的性質》
溫故知新
判定兩條直線平行,我們學過的方法有哪些?
一、定義:同一平面內,兩直線無公共交點。
二、同位角、內錯角相等或同旁內角互補可以判斷兩條線平行。
心靈手巧畫一畫:
借助練習本上的橫線格,畫兩條平行線被第三條直線所截。
探索新知
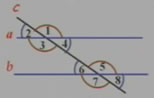
如圖:直線a與直線b平行
(1)圖中有幾對同位角,請分別找出來。
(2)任選其中的一對同位角,用量角器量出它們的度數(shù),并比較它們的大小。
(3)其他同位角的大小也有這種關系嗎?
(4)由此你可得到什么結論?
兩條平行線被第三條直線所截,同位角相等。
簡記:兩直線平行,同位角相等。
類似地,你能得到兩條直線平行時,內錯角之間的關系嗎?
兩直線平行,內錯角相等。
類似地,你能得到兩條直線平行時,同旁內角呢?
兩直線平行,同旁內角互補。
學習重點:平行線的性質
兩直線平行,同位角相等。
兩直線平行,內錯角相等。
兩直線平行,同旁內角互補。
基礎練習
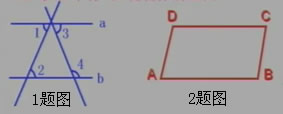
1、如圖,直線a∥b,∠1=54°,則∠2=_____,根據(jù)是_______;∠3=_____,根據(jù)是_______;∠4=_____,根據(jù)是_______。
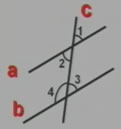
2、如圖,已知直線AB∥CD且被AE所截。
(1)∠1=110°,則∠2=_____。( )
(2)∠1=110°,則∠3=_____。( )
(3)∠1=110°,則∠4=_____。( )
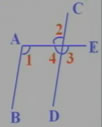
3、如圖,已知AB∥CD,AD∥BC,填空:
(1)∵AB∥CD(已知)
∴∠1=______(兩直線平行,內錯角相等。)
(2)∵AD∥BC(已知)
∴∠2=______( )
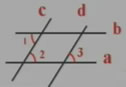
4、如圖:已知直線a∥b,直線c∥d,∠1=70°,則∠2的度數(shù)=____,根據(jù)是___________,∠3的度數(shù)=____,根據(jù)是___________。
實際應用 優(yōu)勢互補
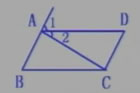
如圖是舉世聞名的三星堆考古中發(fā)掘出的一個殘缺玉片,通過整理發(fā)現(xiàn)這是一塊梯形玉片,量得∠A=115°,∠D=100°。請你求出另外兩個角的度數(shù)。
生活中的數(shù)學
如圖,當兩個人的目光相對時,視線與水平線所成的角相等嗎?為什么?
議一議:
平行線的判定和性質有什么共同點和不同。
綜合應用
性質
判定
由“線”(平行)知“角”(相等或互補)
由“角”(相等或互補)定“線”(平行)
兩直線平行
同位角相等
同位角相等
兩直線平行
內錯角相等
內錯角相等
兩直線平行
同旁內角互補
同旁內角互補
兩直線平行
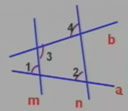
已知:如圖,已知∠1=∠2,∠3=115°。求∠4的度數(shù)。
突破難點
如圖,一束平行光線AB和DE射向一個水平鏡面后被反射。
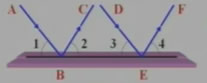
(1)∠1,∠3的大小有什么關系?
(2)反射光線BC與EF也平行嗎?
挑戰(zhàn)自我
1、如圖,已知∠1=∠2,∠3=65°。求∠4的度數(shù)。
2、如圖,已知AD∥BC,∠A=∠C,AB與CD平行嗎?說說你的理由。
感悟反思
本節(jié)課學習了平行線的性質,總結了平行線的判定與性質的區(qū)別。
條件:角的關系→平行關系
特征:平行關系→角的關系
此內容正在抓緊時間編輯中,請耐心等待
李老師
女,中教中級職稱
在教學上能針對數(shù)學學科特點,幫助學生理清各知識點之間聯(lián)系,掌握數(shù)學學科的脈絡。
























