課程內容:
《探索勾股定理(2)》
知識回顧;
1.勾股定理的內容是什么?
2.它反映的是直角三角形中的那些基本量之間的關系?
3,我們是用什么方法得到這個結論的?
如果三角形中兩邊的平方和等于第三邊的平方,那么這個三角形是直角三角形。
即如果三角形的三邊長a,b,c有關系
a2+b2=c2
那么這個三角形是直角三角形。
1 想一想:上述哪條邊所對的角是直角?
2 這個定理可判斷三角形是否是直角三角形
3 能夠成為直角三角形三邊長的三個正整數,稱為勾股數(或勾股弦數)。
例1.根據下列條件,分別判斷以a,b,c為邊的三角形是不是直角三角形。
(1)a=7,b=24,c=25.
(2)a=2/3,b=1,c=2/3
課堂練習:
下列幾組數能否作為直角三角形的三邊長?說說你的理由。
(1)29,21,20
(2)5,7,8
(3)12,35,36
例2:已知△ABC的三邊長分別為a,b,c,且a=m2-n2,b=2mn,c=m2+n2.(m,n是正整數,且m>n),△ABC是直角三角形嗎?請說明理由。
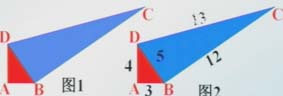
例3:一個零件的形狀如圖1所示,按規定這個零件中∠A和∠DBC都應為直角。個人師傅量得這個零件各邊尺寸如圖2所示,這個零件符合要求嗎?
思考題:
1、四邊形ABCD中已知AB=3,BC=4,CD=12,DA=13,且∠ABC=90°,求這個四邊形的面積。
2、請你寫出三組勾股數;
3、一組勾股數的倍數一定是勾股數嗎?為什么?
4、四邊形ABCD中,∠ACB=90°,AB=13,BC=5,AD=9,CD=15,回答下列問題
(1)AC的長是多少?
(2)△ABC,△ACD是直角三角形嗎?為什么?
(3)這個四邊形的面積是多少?
此內容正在抓緊時間編輯中,請耐心等待
楊老師
男,中教中級職稱
從教20余年,市優秀教師、“教學標兵”,曾在全省、全國青年教師課堂教學大賽中獲獎。
























