課程內容
《集合常用邏輯用語》
真題熱身
1.設集合U=｛1,2,3,4,5,6｝，M=｛1,2,4｝，則CuM=（ C）
A U B ｛1,3,5｝ C ｛3,5,6｝ D ｛2,4,6｝
2.若p是真命題，q是假命題，則下列結論錯誤的是（①②③）
①p∧q是真命題； ②p∨q是假命題 ③′p是真命題 ④′q是真命題
3.設a b∈R,“a=0”是“復數a+bi是純虛數”的（B ）
A 充分不必要條件 B 必要而不充分條件 C 充分必要條件 D 既不充分也不必要條件
故選：B
考點整合
1.集合
（1）集合元素的三個特征：確定性、互異性、無序性，是判斷某些對象能否構成一個集合或判斷兩集合是否相等的依據。
（2）集合的表示方法：列舉法、描述法、圖示法
要特別注意用描述法表示集合時先弄清楚集合的元素是什么，再進行集合間關系的判斷及運算。
（3）集合間的關系：子集、真子集、孔集、集合相等，在集合間的運算中藥注意空集的情形
（4）重要結論
A∩B=A≒A
B; A∪B=A≒B 
A
2.四種命題間的關系
兩個命題互為逆否命題，它們有相同的真假性；
兩個命題為互逆命題或互否命題，它們的真假性沒有關系；
一個命題的逆命題與它的否命題同真同假。
3.含有一個量詞的否定
（1）全稱命題p：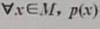
，它的否定：
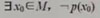是特殊命題；
（2）特稱命題p: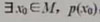
，它的否定：
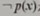是全稱命題
4.充分、必要條件
設集合A=｛x|x滿足條件p｝，B=｛x|x滿足條件q｝，則有
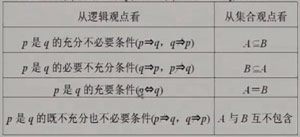
分類突破
一、集合間關系與運算
例 1 若集合A=｛y|y=x3，-1≦x≦1｝，B=﹛x|y=√1-x﹜，則A∩B=[-1,1].
歸納拓展
解答集合間關系與運算問題的一般步驟：先正確理解各個集合的含義，認清集合元素的屬性；再依據元素的不同屬性采用不同的方法對集合進行化簡求解，一般的規律為：
（1）若給定的集合是不等式的解集，用數軸求解；
（2）若給定的集合時點集，用數形結合法求解；
（3）若給定的集合時抽象集合，用Venn圖求解。
變式訓練1
（1）設集合M=｛y|y-m≤0｝，N=﹛y|y=2x次方-1，x∈R﹜，若M∩N≠空集，則實數m的取值范圍為（-1，+∞）
（2）已知集合A=﹛1,3，√m﹜，B=﹛1，m﹜，A∪B=A,則m=（ B）
Ａ 0或√3 B 0或3 C 1或√3 D 1或3
二、邏輯聯結詞、全稱（特稱）命題
例 2 已知命題p：“任意數x∈[1,2]，x2-a2≥0”，命題q：“Ex0∈R，xo2+2axo+2-a=0”，若命題“p且q”是真命題求實數a的取值范圍。
解：由“p且q”是真命題，則p為真命題，q也為真命題
若p為真命題，即x∈[1,2]時，a≤x2恒成立，
∴a≤1.
若q為真命題，即x2+2ax+2-a=0有實根，
∴⊿=4a2-4（2-a）≥0，即a≥1或a≤-2
綜上，所求實數a的取值范圍為a≤-2或a=1.
歸納拓展
含有邏輯聯結詞的命題要首先確定構成命題的（一個或兩個）命題的真假，求出此時參數成立的條件，再求出含邏輯聯結詞的命題成立的條件。
三、充分，必要條件
例 2 已知p：x2-8x-20≦0，q：x2-2x+1-m2≤0（m＞0），且非p是非q的必要不充分條件，求實數m的取值范圍。
解 由x2-8x-20≦0，得-2≤x≤10，
由x2-2x+1-m2≤0（m＞0），得1-m≤x≤1+m
∵非p是非q的必要不充分條件，
∴q是p的必要不充分條件，即p是q的充分不必要條件
即p可以推出q，但q不可以推出p，
∴﹛x|-2≤x≤10﹜是﹛x|1-m≤x≤1+m﹜的真子集
∴1-m≤-2,1+m≥10,解得m≥9
∴實數m的取值范圍為﹛m|m≥9﹜
歸納拓展 一般地，在設計到求字母參數的取值范圍的充要條件的問題中，常常要利用集合的包含，相等關系來考慮，非p與非q是兩個非空的數集，非p是非q的必要而不充分條件，即非q可以推出非q，深刻理解這一點，是解決本例的關鍵。另外，一個命題與它的逆否命題是等價命題，故常將非p是非q的必要不充分條件，等價轉化為q是p的必要不充分條件。
變式訓練3
命題甲：x≠2或y≠3；命題乙：x+y≠5，則甲是乙的（必要不充分）條件。
規范演練
一 填空題
１．設全集為Ｒ，集合Ａ＝﹛x|-1＜x＜1﹜，B=﹛x|x≥0﹜，則CR（A∪B）=﹛x|x≤-1﹜
2.已知命題p：自然數n∈N，2的n次方＞1000，則非p為任意數n∈N,2的n次方≤1000
解析：由于存在性命題的否定是全稱命題，因而非p為任意數n∈N,2的n次方≤1000
此內容正在抓緊時間編輯中，請耐心等待
孫老師
女，中教高級職稱
優秀教師，高級教師職稱。善于引導、啟發學生，培養學生的邏輯思維，激發孩子對數學學習的興趣。
