課程內(nèi)容
《頻率的穩(wěn)定性》(2)
回顧與思考
1、舉例說(shuō)明什么是必然事件。
2、舉例說(shuō)明什么是不可能事件。
1、舉例說(shuō)明什么是不確定事件。
問(wèn)題的引出
拋擲一枚均勻的硬幣,硬幣落下后,會(huì)出現(xiàn)兩種情況:
正面朝上 正面朝下
你認(rèn)為正面朝上和正面朝下的可能性相同嗎?
游戲環(huán)節(jié):擲硬幣實(shí)驗(yàn)
(1)同桌兩人做20次擲硬幣的游戲,并將記錄記載在下表中。
(2)累計(jì)全班同學(xué)的試驗(yàn)結(jié)果,并將試驗(yàn)數(shù)據(jù)匯總填入下表:
(3)根據(jù)上表,完成下面的折線統(tǒng)計(jì)圖。
實(shí)驗(yàn)總次數(shù)
20
40
60
80
100
120
140
160
180
200
正面朝上的次數(shù)
正面朝上的頻率
正面朝下的次數(shù)
正面朝下的頻率
真知灼見(jiàn),源于實(shí)踐
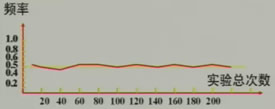
(4)觀察上面的折線統(tǒng)計(jì)圖,你發(fā)現(xiàn)了什么規(guī)律?
當(dāng)實(shí)驗(yàn)的次數(shù)較少時(shí),折線在“0.5水平直線”的上下擺動(dòng)的幅度較大;隨著實(shí)驗(yàn)的次數(shù)的增加,折線在“0.5水平直線”的上下擺動(dòng)的幅度會(huì)逐漸變小。
當(dāng)試驗(yàn)次數(shù)很大時(shí),正面朝上的頻率折線差不多穩(wěn)定在“0.5水平直線”上。
歷史上擲硬幣試驗(yàn)
表中的數(shù)據(jù)支持你發(fā)現(xiàn)的規(guī)律嗎?
試驗(yàn)者
投擲次數(shù)n
正面出現(xiàn)次數(shù)m
正面出現(xiàn)的頻率m/n
布豐
4040
2048
0.5069
德·摩根
4092
2048
0.5005
費(fèi)勒
10000
4979
0.4979
皮爾遜
12000
6019
0.5016
皮爾遜
24000
12012
0.5005
維尼
30000
14994
0.4998
羅曼諾夫斯基
80640
39699
0.4923
學(xué)習(xí)新知
1、在實(shí)驗(yàn)次數(shù)很大時(shí)事件發(fā)生的頻率,都會(huì)在一個(gè)常數(shù)附近擺動(dòng),這個(gè)性質(zhì)稱(chēng)為頻率的穩(wěn)定性。
2、我們把這個(gè)刻畫(huà)事件A發(fā)生的可能性大小的數(shù)值,稱(chēng)為事件A發(fā)生的概率,記為P(A)。
一般的,大量重復(fù)的實(shí)驗(yàn)中,我們常用不確定事件A發(fā)生的頻率來(lái)估計(jì)事件A發(fā)生的概率。
想一想
事件A發(fā)生的概率P(A)的取值范圍是什么?必然事件發(fā)生的概率是多少?不可能事件發(fā)生的概率又是多少?
必然事件發(fā)生的概率為1;不可能事件發(fā)生的概率為0;不確定事件A發(fā)生的概率P (A)是0與1之間的一個(gè)常數(shù)。
所以在拋硬幣試驗(yàn)中:
P(正面朝上)=0.5
p(正面朝下)=0.5
小試牛刀
對(duì)某批乒乓球的質(zhì)量進(jìn)行隨機(jī)抽查,如下表所示:
(1)完成上表。
隨機(jī)抽取的乒乓球數(shù)n
10
20
50
100
200
500
1000
優(yōu)等品數(shù)m
7
16
43
81
164
414
825
優(yōu)等品率m/n
(2)根據(jù)上表,在這批乒乓球中任取一個(gè),它為優(yōu)等品的概率是多少?
(3)如果重新再抽取1000個(gè)乒乓球進(jìn)行質(zhì)量檢查,對(duì)比上表記錄下數(shù)據(jù),兩表的結(jié)果會(huì)一樣嗎?為什么?
是“玩家”就玩出水平
請(qǐng)選擇一個(gè)你能完成的任務(wù),并預(yù)祝你能出色地完成任務(wù):
智慧版
1、下列事件發(fā)生的可能性為0的是( )
A、擲兩枚骰子,同時(shí)出現(xiàn)數(shù)字“6”朝上
B、小明從家里到學(xué)校用了10分鐘,從學(xué)校回到家里卻用了15分鐘
C、今天是星期天,昨天必定是星期六
D、小明步行的速度是每小時(shí)40千米
2、口袋中有9個(gè)球,其中4個(gè)紅球,3個(gè)藍(lán)球,2個(gè)白球,在下列事件中,發(fā)生的可能性為1的是( )
A、從口袋中拿一個(gè)球恰為紅球
B、從口袋中拿出2個(gè)球都是白球
C、拿出6個(gè)球中至少有一個(gè)球是紅球
D、從口袋中拿出的球恰為3紅2白
3、小凡做了5次拋擲均勻硬幣的實(shí)驗(yàn),其中有3次正面朝上,2次正面朝下,他認(rèn)為正面朝上的概率大約為3/5,朝下的概率為2/5,你同意他的觀點(diǎn)嗎?你認(rèn)為他再多做一些實(shí)驗(yàn),結(jié)果還是這樣嗎?
超人版
1、給出以下結(jié)論,錯(cuò)誤的有( )
①如果一件事發(fā)生的機(jī)會(huì)只有十萬(wàn)分之一,那么它就不可能發(fā)生。②如果一件事發(fā)生的機(jī)會(huì)達(dá)到99.5%,那么它就必然發(fā)生。③如果一件事不是不可能發(fā)生的,那么它就必然發(fā)生。④如果一件事不是必然發(fā)生的,那么它就不可能發(fā)生。
A、1個(gè) B、2個(gè) C、3個(gè) D、4個(gè)
2、小明拋擲一枚均勻的硬幣,正面朝上的概率為1/2,那么,拋擲100次硬幣,你能保證恰好50次正面朝上嗎?
3、把標(biāo)有號(hào)碼1,2,3,……,10的10個(gè)乒乓球放在一個(gè)箱子中,搖勻后,從中任意取一個(gè),號(hào)碼為小于7的奇數(shù)的概率是________
行家看”門(mén)道”
擲一枚均勻的骰子。
(1)會(huì)出現(xiàn)哪些可能的結(jié)果?
(2)擲出點(diǎn)數(shù)為1與擲出點(diǎn)數(shù)為2的可能性相同嗎?
擲出點(diǎn)數(shù)為1與擲出點(diǎn)數(shù)為3的可能性相同嗎?
(3)每個(gè)出現(xiàn)的可能性相同嗎?你是怎樣做的?
回味無(wú)窮
1、頻率的穩(wěn)定性。
2、事件A的概率,記為P(A)。
3、一般的,大量重復(fù)的實(shí)驗(yàn)中,我們常用不確定事件A發(fā)生的頻率來(lái)估計(jì)事件A發(fā)生的概率。
4、必然事件發(fā)生的概率為1;
不可能事件發(fā)生的概率為0;
不確定事件A發(fā)生的概率P(A)是0與1之間的一個(gè)常數(shù)。
此內(nèi)容正在抓緊時(shí)間編輯中,請(qǐng)耐心等待
馬老師
女,中教高級(jí)職稱(chēng)
從教30年,數(shù)學(xué)教研組長(zhǎng),市級(jí)骨干教師。曾在全國(guó)青年教師課堂教學(xué)大賽中獲獎(jiǎng),具有豐富的數(shù)學(xué)教學(xué)經(jīng)驗(yàn)。
























