課程內容
《線段的垂直平分線》(2)
線段垂直平分線的性質定理:
線段垂直平分線上的點到這條線段的兩個端點的距離相等。
數學語言:
∵EF⊥AB AO=BO
(或EF垂直平分AB)
點P在EF上
∴PA=PB
請寫出上面定理的逆命題
線段垂直平分線上的點到這條線段的兩個端點的距離相等。
如果一個點在一條線段的垂直平分線上,那么這個點到這條線段的兩個端點的距離相等。
如果一個點到一條線段的兩個端點的距離相等,那么這個點在這條線段垂直平分線上。
填寫下面命題證明過程的理由:
已知:如圖,P為線段AB外的一點,且PA=PB。
求證,點P在線段AB的垂直平分線上。
證明:過點P作直線EF⊥AB,垂足為O,則
∠POA=∠POB=90°(垂直定義)
在Rt△PAO和Rt△PBO中,
PA=PB(已知),PO=PO(公共邊)
∴Rt△PAO≌Rt△PBO(HL)
∴AO=BO(全等三角形的對應相等)
∴EF是線段AB的垂直平分線(線段垂直平分線的定義)
∴點P在線段AB的垂直平分線上。
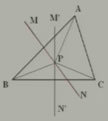
例1 已知,如圖,在△ABC中,邊AB,BC的垂直平分線交于P。
求證:PA=PB=PC。
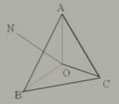
例2 已知:在△ABC中,ON是AB的垂直平分線,OA=OC。
求證:點O在BC的垂直平分線上。
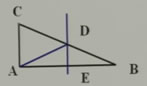
例3 在△ABC中,DE垂直平分AB,AB=8cm,△ACD的周長為10cm。求△ABC的周長。
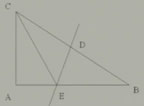
例4 如圖:在Rt△ABC中,∠A=90°,線段BC的垂直平分線DE,如果CE恰好是∠ACB的平分線,求∠B的度數。
例5 如圖:AB=AD,BC=DC,E是AC一點。
求證:BE=DE。

試一試
方便居民的生活,市政府計劃在三個住宅小區A、B、C之間修建一個購物中心,試問,該購物中心應建于何處,才能使得它到三個小區的距離相等。
實際問題→數學化
求作一點P,使它和△ABC的三個頂點距離相等。
求作:作線段AB的垂直平分線。
作法:
1、分別以點A和B為圓心,以大于AB/2長為半徑作弧,兩弧交于點C和D。
2、作直線CD。
則直線CD就是線段AB的垂直平分線。
請你說明CD為什么是AB的垂直平分線,并與同伴進行交流。
此內容正在抓緊時間編輯中,請耐心等待
王老師
女,中教高級職稱
從事數學教學與研究多年,市優秀教師、優秀班主任。獲市“優秀課”獎、“教學能手”稱號。
























