課程內容
《應用二元一次方程組——雞兔同籠》
學習目標
1、使學生初步掌握列二元一次方程組解應用題的方法與步驟。
2、通過將實際問題轉化成純數學問題的應用訓練,培養學生分析問題、解決問題的能力。
3、通過對祖國文明史的了解,培養學生愛國主義精神,樹立為中華崛起而學習的信心。
雞兔同籠
今有雞兔同籠,
上有三十五頭,
下右九十四足,
問雞兔各幾何?
“雞兔同籠”是一類有名的中國古算題,最早見于《孫子算經》下卷第31題“雉兔同籠”,流傳廣泛,許許多多數學應用題都可以轉化成這類問題來解決,或者用解決“雞兔同籠”問題的解法來解決。
“雉兔同籠”題:今有雉(雞)兔同籠,上有35頭,下有94足,問雉兔各幾何?
(1)《孫子算經》中記載的算法:
金雞獨立,兔子站起
數腳:94÷2=47(只)
頭數:兔 47-35=12(只)
雞 35-12=23(只)
總腳數÷2-總頭數=兔子數
能夠這樣算,主要是利用了兔和雞的腳數分別是4和2,4又是2的倍數。可是當其他問題轉化成這類問題時,數就不一定是4和2,上面的計算方法就行不通。
1、“上有35頭”的意思是什么?“下有94足”呢?
2、你能根據(1)中的數量關系列出方程嗎?
3、你能解決這個有趣的問題嗎?
解:設籠中有雞x只,有兔y只,由題意可得:
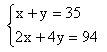
解此方程組得: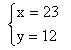
答:籠中有雞23只,兔12只。
例1:以繩測井。若將繩三折測之,繩多五尺;若將繩四折測之,繩多一尺。繩長、井深各幾何?
題目大意:用繩子測水井深度,如果將繩子折成三等份,一份繩長比井深多5米;如果將繩子折成四等份,一份繩長比井深多1尺。問繩長、井深各是多少尺?
等量關系:
(井深+5)×3=繩長
(井深+1)×4=繩長
解:設繩長x尺,井深y尺,則由題意得
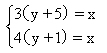
解此方程組得: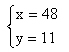
所以繩長48尺,井深11尺。
練習
1、設甲數為x,乙數為y,則甲數的2倍與乙數的3倍的和為15,列出方程為__________。
2、一只蛐蛐6條腿,一只蜘蛛8條腿,現有蛐蛐和蜘蛛共10只,共有68條腿,若設蛐蛐有x只,蜘蛛有y只,則列出方程組__________。
3、小剛有5角硬幣和一元硬幣有8枚,幣值共有6元5角,設5角的有x枚,一元的有y枚,列出的方程組為__________。
4、甲、乙兩人參加植樹活動,兩人共植樹20棵,已知甲植樹數是乙的1.5倍。如果設甲植樹x棵,乙植樹y棵,那么可列方程組為( )
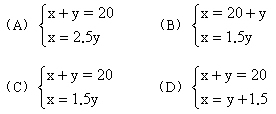
5、做一做:
列方程組解古算題:
“今有牛五、羊二,直金十兩。牛二、羊五,直金八兩。牛、羊各直金幾何?”
題目大意是:5頭牛、2只羊共價值10兩“金”。2頭牛、5只羊共價值8兩“金”。每頭牛、每只羊各價值多少“金”?
6、買一些4分和8分的郵票,共花6元8角,已知8分的郵票比4分的郵票多40張,那么兩種郵票各買了多少張?
此內容正在抓緊時間編輯中,請耐心等待
馬老師
男,中教高級職稱
省級骨干教師,市教育學會會員,校教務科副科長,年級組長。廣愛并濟,善待每個學生,因此深受學生愛戴。
























