榴莲视频官网_国产尤物精品视频_在线成年人视频_国产一区二区三区夜色

課程內容

《橢圓及其標準方程（二）》
復習舊知
1、橢圓的定義：
平面內與兩個定點F₁F₂的距離和等于常數（大于F₁F₂）的點的軌跡叫作橢圓，這兩個定點叫做橢圓的焦點，兩焦點間的距離叫做橢圓的焦距。
注：若P是橢圓的點，則
|PF₁|+|PF₂|=2a
2、橢圓的標準方程

定義	|MF1|+|MF2|=2a(2a>2c>0)
圖形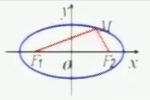
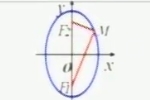方程	x2/a2+y2/b2=1(a>b>0)	y2/a2+x2/b2=1(a>b>0)
焦點	F1（-c,0）,F2(c,0)	F1(0,-c),F2(0,c)
a、b、c之間的關系	a2-c2=b2(a>b>c>0,a>b>0)

注：焦點位置的判斷
看分母的大小，焦點在分母大的那一項對應的坐標軸上。
舊知測試：
1、如果方程x²+ky²=1表示焦點在y軸上的橢圓，那么實數k的取值范圍是（D）
A、（0，+∞）
B（0,2）
C、（1，+∞）
D（0,1）
2、橢圓x²/25+y²/9=1一點P到一個焦點的距離為5，則P到另一個焦點的距離（A）
A、5   B、6   C、4   D、10
3、橢圓x²/25+y²/169=1的焦點坐標是（C）
A(±5,0)   B（0，±5）   C（0，±12）    D（±12,0）
4、已知橢圓方程為x²/23+y²/32=1，則這個橢圓的焦距為（A）
A、6   B、3   C、3√5   D、8
5、F₁F₂是定點，且|F₁F₂|=6，動點M滿足|MF₁|+|MF₂|=6，則點M的軌跡是（D）
A、橢圓
B、直線
C、圓
D、線段
例1：如圖，設點A、B的坐標分別為（-5,0）（5，0），直線AM，BM相較于點M，且它們的斜率之積是-4/9，求點M的軌跡方程。

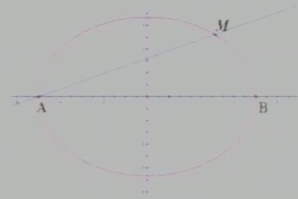
解：設M（x,y）
由題可得：
y/(x=5)·y/(x-5)=-(4/9)
y²/(x²-25)=-(4/9)
9y²=100-4x²
9y²⁺4x²=100
∴點M的軌跡方程為：x²/25+y²/(100/9)=1
例2、如圖，在圓x²+y²=4上任取一點P作x軸的垂線段PD，D為垂足。當點P在圓上運動時，線段PD的中點M的軌跡是什么？為什么？
解：設點M坐標為M（x,y），點P的坐標為P(x',y'),則
由提議可得：x'=x,y'=y
因為x'²+y'²=4
所以x²+4²y=4即x/4+y=1
這就是點M的軌跡方程，它表示一個橢圓。
例3、已知B、C兩個定點，|BC|=6且三角形ABC的周長為16，求頂點A的軌跡方程。
變式1：已知B（-3,0），C（3,0），|CA|、|BC|、|AB|成等差數列，求三角形ABC的頂點A的軌跡方程。
變式2：已知已知B（-3,0），C（3,0）且sinB+sinC=2sinA，求三角形ABC的頂點A的軌跡方程。
變式3：一動圓與已知圓O：（x+3）+y=1外切，與圓O：（x-3）+y=81內切，試求這動圓圓心的軌跡方程。