榴莲视频官网_国产尤物精品视频_在线成年人视频_国产一区二区三区夜色

課程內(nèi)容
《橢圓的簡單幾何性質(zhì)(一)》
教學(xué)目的：
1、熟練掌握橢圓的范圍，對稱性，頂點(diǎn)等簡單幾何性質(zhì)
2、掌握標(biāo)準(zhǔn)方程中a，b，c的幾何意義，以及a，b，c，e的相互關(guān)系
3、理解、掌握坐標(biāo)法中根據(jù)曲線的方程研究曲線的幾何性質(zhì)的一般方法
教學(xué)重點(diǎn)：橢圓的幾何性質(zhì)
教學(xué)難點(diǎn)：如何貫徹數(shù)形結(jié)合思想，運(yùn)用曲線方程研究幾何性質(zhì)
復(fù)習(xí)：
1、橢圓的定義：
平面內(nèi)與兩個定點(diǎn)F_1、F₂的距離和等于常數(shù)（大于F₁F₂）的點(diǎn)的軌跡叫作橢圓。
|PF₁|+|PF₂|=2a（2a>|F₁F₂|）
2、橢圓的標(biāo)準(zhǔn)方程是：
當(dāng)焦點(diǎn)在X軸上時：x²/a²+y²/b²=1(a>b>0)
當(dāng)焦點(diǎn)在Y軸上時：y²/a²+x²/b²=1(a>b>0)
3、橢圓中a，b，c的關(guān)系是：
a²=b²+c²

	焦點(diǎn)在X軸上	焦點(diǎn)在Y軸上
不同點(diǎn)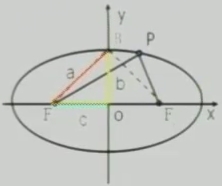
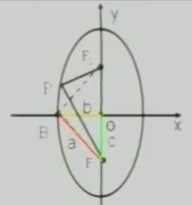	F1（-c，0）F2(c,0)	F1（0,-c）F2(0,c)
	x2/a2+y2/b2=1(a>b>0)	y2/a2+x2/b2=1(a>b>0)
相同點(diǎn)	定義：PF1+PF2=2a
	參數(shù)：a2=b2+c2（a>b>0  a>c>0）

二、橢圓x²/a²+y²/b²=1簡單的幾何性質(zhì)
1、范圍：x²/a²≤1，y²/b^2≤1得：
-a≤x≤a，-b≤y≤b知
橢圓落在x=±a，y=±b組成的矩形中

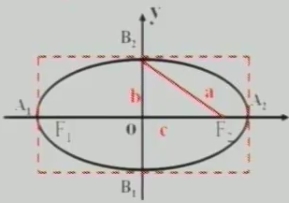
2、橢圓的對稱性
從圖形上看，拖延關(guān)于X軸，Y軸、原點(diǎn)對稱。
從方程上看：
（1）把X換成-X方程不變，圖象關(guān)于Y軸對稱；
（1）把Y換成-Y方程不變，圖象關(guān)于X軸對稱；
（1）把X換成-X方程不變，同時把把Y換成-Y方程不變，圖象關(guān)于原點(diǎn)成中心對稱。
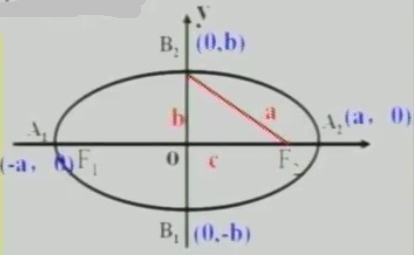
3、橢圓的頂點(diǎn)
x²/a²+y²/b²=1(a>b>0)
令X=0，得Y=？，說明橢圓與Y軸的交點(diǎn)？
令Y=0，得X=？說明橢圓與X軸的交點(diǎn)？
頂點(diǎn)：橢圓與它的對稱軸的四個交點(diǎn)，叫做橢圓的頂點(diǎn)。
長軸、短軸：線段A₁A₂、B₁B₂分別叫做橢圓的長軸和短軸。
a、b分別叫做橢圓的長半軸長和短半軸長。

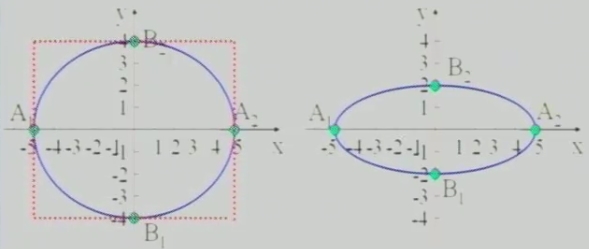
根據(jù)前面所學(xué)有關(guān)知識畫出下列圖形
（1）x²/25+y²/16=1
（2）x²/25+y²/4=1

4、橢圓的離心率e（刻畫橢圓扁平程度的量）
離心率：橢圓的焦距與長軸長的比：e=c/a叫做橢圓的離心率。
（1）離心率的取值范圍：0 （2）離心率對橢圓形狀的影響：
1）e越接近1，c就越接近a，從而b就越小，橢圓就越扁。
2）e越接近0，c就越接近0，從而b就越大，橢圓就越圓。
思考：當(dāng)e=0時，曲線是什么？當(dāng)e=1時，曲線又是什么？
|3|e與a,b的關(guān)系：e=c/a=√（(a-b)/c）=對（1-b/a）
問：對于橢圓C₁：9x²+y²=36與橢圓C₂：x²/16+y²/12=2更接近于圓的是：C₂

標(biāo)準(zhǔn)方程	x2/a2+y2/b2=1(a>b>0) y2/a2+x2/b2=1(a>b>0)
范圍	|x|≤a，|y|≤b
對稱性	關(guān)于x軸對稱，y軸成軸對稱；關(guān)于原點(diǎn)成中心對稱
頂點(diǎn)坐標(biāo)	（a，0）（-a,0）,(0,b)(0,-b)
焦點(diǎn)坐標(biāo)	（c,0）、(-c,0)
半軸長	長半軸長為a，短半軸長尾b,a＞b
離心率	e=c/a
a、b、c的關(guān)系	a2=b2+c2

例1、已知橢圓方程為16x²+25y²=400，則它的長軸長是：10；短軸長是：8；焦距是：6；離心率等于：3/5；焦點(diǎn)坐標(biāo)是：（±3,0）；頂點(diǎn)坐標(biāo)是：（±5,0）（0，±4）：外切矩形的面積等于：80；