2021年人教版八年級數(shù)學上冊第13章《軸對稱》13.4 課題學習——最短路徑問題
一、單選題
1.在等邊三角形ABC 中,D,E分別是BC,AC的中點,點P是線段AD上的一個動點,當△PCE的周長最小時,Р點的位置在( )
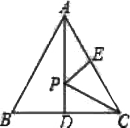
A. A點處
B. D點處
C. AD的中點處
D. △ABC三條高的交點處
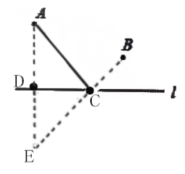
2.如圖,點A,B是直線l同側(cè)不重合的兩點,在直線l上求作一點C,使得AC+BC的長度最短.作法︰①作點B關(guān)于直線的對稱點B';②連接AB',與直線l相交于點C,則點C為所求作的點.在解決這個問題時沒有用到的知識或方法是( )
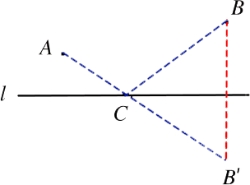
A.轉(zhuǎn)化思想
B.三角形兩邊之和大于第三邊
C.兩點之間,線段最短
D.三角形的一個外角大于與它不相鄰的任意一個內(nèi)角
4.在平面直角坐標系中,點A、B的坐標分別為(2,0),(4,0),點C的坐標為(m,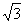 m) (m為非負數(shù)),則CA+CB的最小值是( )
m) (m為非負數(shù)),則CA+CB的最小值是( )
B.
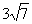
C.
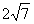
D. 5
二、填空題
三、按要求作圖

此內(nèi)容正在抓緊時間編輯中,請耐心等待
崔老師
男,中教高級職稱
市優(yōu)秀教師、骨干教師,數(shù)學學科帶頭人。在教學中注重學生自學能力和數(shù)學思維能力的培養(yǎng),教學成績突出。




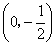
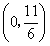
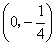
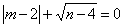 ,且m、n恰好是等腰
,且m、n恰好是等腰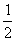 BC,則△ABC的頂角的度數(shù)為.
BC,則△ABC的頂角的度數(shù)為.