榴莲视频官网_国产尤物精品视频_在线成年人视频_国产一区二区三区夜色

課程內容：

《直角三角形（二）》

直角三角形的性質2：

直角三角形斜邊上的中線等于斜邊的一半

數學語言表述為：

在Rt△ABC中
∵CD是斜邊AB上的中線
∴CD=AD=BD=1/2AB

練一練：

1、已知Rt△ABC中，斜邊AB=10cm,則斜邊上的中線的長為________

2、在Rt△ABC中，CD是斜邊AB上的中線，∠CDA=80°，則∠A=_____∠B=______

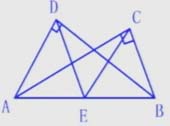
例1：如圖，已知AD⊥BD，AC⊥BC，E為AB的中點，試判斷DE與CE是否相等，并說明理由。

變式題：已知AD。BE分別是△ABC的BC、AC邊上的高，F是DE的中點，G是AB的中點，則FG⊥DE，請說明理由。

思考：

在Rt△ABC中，BD是斜邊AC上的中線，∠A=30°
（1）∠C=_____∠ABD=____
∠BDC=______∠CBD=_____
（2）△BDC是什么三角形？
（3）此時BC與AC有什么關系？

直角三角形的性質3：

在直角三角形中，30°角所對的直角邊等于斜邊的一半。

練一練：

1 在Rt△ABC中∠A=30°，AB+BC=12cm,則AB=_______cm

2 △ABC是等邊三角形，D,E分別在BC和AC上，AD⊥BC，DE⊥AB,若AB=8cm,BD=____,BE=_____

3 一名滑雪運動員沿著斜角為30°的斜坡，從A滑行至B。已知AB=200m,問這名滑雪運動員的高度下降了多少m?

4 在△ABC中，AB=AC=2a,∠ABC=∠ACB=15°，CD是腰AB上的高，求CD的長。