榴莲视频官网_国产尤物精品视频_在线成年人视频_国产一区二区三区夜色

課程內(nèi)容：

《實數(shù)的概念（1）》
探究：
歸納：事實上，任何一個有理數(shù)都可以化成有限小數(shù)或無限循環(huán)小數(shù)。反過來，任何有限小數(shù)或無限循環(huán)小數(shù)，都是有理數(shù)。
練習：前幾節(jié)課，我們曾經(jīng)把兩個面積為1的小正方形沿對角線剪開，將所得的4個直角三角形拼在一起，就得到一個面積為2的大正方形。你知道這個大正方形的變長是多少嗎？
     設大正方形的邊長為x，則
     x₂=2    所以，根據(jù)算術平方根的意義可知
     x=√2

定義：很多數(shù)的平方根和立方根都是無限不循環(huán)小數(shù)，無限不循環(huán)小數(shù)又叫做無理數(shù)。有理數(shù)和無理數(shù)統(tǒng)稱實數(shù)。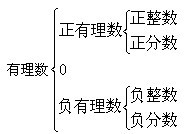
         

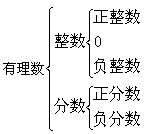
練習：把下列各數(shù)填入相應的集合內(nèi)：
    ｜-√9｜  ^3√2  √81  3∏  0.7循環(huán)  -3/4  ^3√-9   6    3.14
（1）整數(shù)集合{    …}
（2）分數(shù)集合{    …}
（3）負數(shù)集合{    …}
（4）有理數(shù)集合{    …}
（5）無理數(shù)集合{    …}
（6）實數(shù)集合{    …}
思考：直徑為1個單位長度的圓從原點沿數(shù)軸向右滾動一周，圓上的一點由原點到達點o'，點o'的坐標是多少？
歸納：實數(shù)與數(shù)軸上的點一一對應。即每一個實數(shù)都可以用數(shù)軸上的一個點來表示；反之，數(shù)軸上的每一點都表示一個實數(shù)。
      同樣地，平面直角坐標系內(nèi)的點與有序?qū)崝?shù)對是一一對應的。
練習：判斷對錯
    1.無理數(shù)都是無限小數(shù)。（  ）
    2.無限小數(shù)都是無理數(shù)。（  ）
    3.實數(shù)不是有理數(shù)就是無理數(shù)。（  ）
    4.帶根號的數(shù)都是無理數(shù)。（  ）
    5.無理數(shù)一定都帶根號。（  ）
    6.數(shù)軸上的任意一點都可以用實數(shù)表示。（  ）
    7.兩個無理數(shù)之和一定是無理數(shù)。（  ）
我們的收獲：
    ●學習了無理數(shù)和實數(shù)的概念
    ●實數(shù)的分類
    ●數(shù)軸上的點與實數(shù)的一一對應關系以及平面直角坐標系內(nèi)的點與有序?qū)崝?shù)對也是一一對應的關系。