課程內容
高中物理復習課第五章《曲線運動》(必修2)
1.運動的合成和分解 Ⅱ
2.拋體運動 Ⅱ
3.勻速圓周運動、角速度、線速度、向心加速度 I
4.勻速圓周運動的向心力 Ⅱ
5.離心現象 I
基礎知識梳理
一、曲線運動
1.曲線運動的特點
在曲線運動中,運動質點在某一點的瞬時速度的方向就是通過曲線的這一點切線方向,因此質點在曲線運動中速度的方向時刻在變化,所以曲線運動一定是變速運動,但是,變速運動不一定是曲線運動,直線運動中速度大小變化時也是變速運動。
2.做曲線運動的條件
(1)從運動學角度,物體的加速度方向跟速度方向不在同一條直線上時,物體就做曲線運動。
(2)從動力學角度,如果物體所受合外力的方向跟物體的速度方向不在同一條直線上時,物體就做曲線運動。
二、運動的合成和分解
1.合成與分解的概念
已知分運動求和運動稱為運動的合成;已知和運動求分運動為運動的分解,兩者互為逆運算,運動的合成與分解是指描述運動的各種物理量,即位移,速度、加速度的合成與分解。
2.遵循的法則
由于描述運動的各物理量都是矢量,故不再同一條直線上的兩個分運動合成時遵循平行四邊形定則;分解時常用的方法有根據運動的實際效果分解或正交分解。
3.合運動和分運動的關系
(1)等時性:合運動與分運動經歷的時間相等。
(2)獨立性:一個物體同時參與幾個分運動時,各分運動獨立進行,不受其他分運動的影響。
(3)等效性:各分運動疊加起來與合運動有完全相同的效果。
例 1
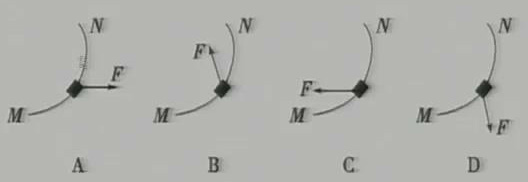
我國“嫦娥一號”探月衛星經過無數人的協作和努力,終于在2007年10月24日18時05分發射升空,如圖所示,“嫦娥一號”探月衛星在由地球飛向月球時,沿曲線從M點到N點的飛行過程中,速度逐漸減小,在此過程中探月衛星所受合力的方向可能是(C)
例 1、 一條自西向東的河流,南北兩岸分別有兩個碼頭A、B,如圖示,已知河寬為80m,河水流速為5m/s,兩個碼頭A、B沿水流的方向相距100m,現有一只船,它在靜水中的行駛速度為4m/s,若使用這只船渡河,且沿直線運動,則(B )
![]()
A 它可以正常來往于A、B兩個碼頭
B 它只能從A 駛向B,無法返回
C 它只能從B 駛向A,無法返回
D 無法判斷
三、平拋運動

例3、平拋運動的兩個重要推論
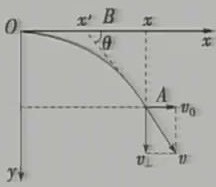
(1)推論 I:做平拋(或類平拋)運動的物體在任意時刻任一位置處,設其末速度方向與水平方向的交角為θ,位移與水平方向的交角為Φ,則tanθ =2tanΦ
(2)推論 Ⅱ:做平拋(或類平拋)運動的物體,任意時刻的瞬時速度方向的方向延長線一定通過此時水平位移的中點,如圖所示。
四、圓周運動

例 4
如圖所示,輕桿的一端有一個小球,另一端有光滑的固定軸O,現給球一初速度,使球和桿一起繞軸,O在豎直面內轉動,不計空氣阻力,用F表示球到達最高點時桿對小球的作用力,則F(D )
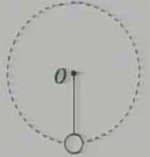
A 一定是拉力
B 一定是推力
C 一定等于0
D 可能使拉力,可能使推力,也可能等于0
此內容正在抓緊時間編輯中,請耐心等待
王老師
女,中教高級職稱
一直擔任高中物理的教學工作,有清晰的理性思維,豐富的高考備考經驗,教學方式嚴謹、活潑。