課程內容
《探索全等三角形全等的條件(1)》
1、全等三角形有哪些性質?
全等三角形對應邊相等,對應角相等。
2、如圖,△ABC≌△DEF,你能得出哪些結論?
∠A=∠D,∠B=∠E,∠C=∠F,AB=DE,BC=EF,AC=DF
六個條件同時滿足的兩個三角形一定全等。如果只滿足六個條件中的一部分條件的兩個三角形全等嗎?
探究一:如果滿足上面六個條件中的一個條件(如一個角對應相等或一條邊對應相等)兩個三角形一定全等嗎?不一定全等
探究二:如果滿足上面六個條件中的兩個條件(如兩個角對應相等或兩條邊對應相等或一條邊和一個角對應相等)兩個三角形一定全等嗎?不一定全等
探究三:如果滿足上面六個條件中的三個條件兩個三角形一定全等嗎?
(如1、三個角都對應相等
2、三條邊對應相等
3、兩條邊和一個角對應相等
4、兩個角和一條邊對應相等)
任意畫一個△ABC,再畫一個△A′B′C′,AB=A′B′,BC=B′C′,CA=C′A′,判斷兩個三角形是否全等?
三角形全等判定一
三邊對應相等的兩個三角形全等(簡寫:“邊邊邊”或“SSS”)
三角形的三邊長度固定,這個三角形的形狀大小就完全確定,這個性質叫三角形的穩定性。
例1:如圖△ABC是一個鋼架,AB=AC,AD是連結點A和BC中點的支架,求證△ABD≌△ACD。
例2:怎樣用直尺和圓規,做一個角等于已知角呢?
已知∠AOB,求作:∠A′O′B′使∠A′O′B′=∠AOB。
作法:1、以O點為圓心,任意長為半徑畫弧,分別交OA,OB于點C、D;
2、畫一條射線O′A′,以點O′為圓心,OC長為半徑畫弧,交O′A′于點C′;
3、以點C′為圓心,CD長為半徑畫弧,與第2步中所畫的弧交于點D′。
4、過點D′畫射線O′B′,則∠A′O′B′=∠AOB
練習
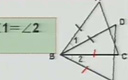
1、如圖,已知AC=FE,BC=DE,點A、D、B、F在一條直線上,AD=FB。要用“邊邊邊”證△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,還應該有什么條件?怎樣才能得到這個條件?
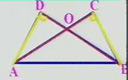
2、如圖,已知AB=CD,AD=CB,求證:∠B=∠D。
此內容正在抓緊時間編輯中,請耐心等待
王老師
男,中教高級職稱
從事了多年的教學工作,積累了豐富的教學經驗。教學風格幽默風趣,善于根據學生的思路進行恰當的引導。