課程內(nèi)容
第26章《反比例函數(shù)》26.1.2 反比例函數(shù)的圖象與性質(1)
知識回顧
1、什么是反比例函數(shù)?
一般地,形如y=k/x(k為常數(shù),k≠0)的函數(shù)叫做反比例函數(shù)。
2、反比例函數(shù)的定義中需要注意什么?
(1)k是非零常數(shù)。
(2)xy=k。
知識回顧
(1)任意寫一個在第二象限的點的坐標:________。
(2)直線y=-x+3經(jīng)過第_____象限。
(3)已知矩形的面積為6,則它的長y與寬x之間的函數(shù)關系式為________,y是x的_____函數(shù)。
(4)若函數(shù)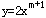 是反比例函數(shù),則m=________。
是反比例函數(shù),則m=________。
(5)反比例函數(shù)y=4/x經(jīng)過點(1,___)。
新課導入
1、一次函數(shù)的圖象與性質是怎樣的?
2、二次函數(shù)的圖象與性質是怎樣的?
3、如何畫函數(shù)的圖象?
描點法:列表→描點→連線
想一想:反比例函數(shù)的圖象與性質又是怎樣的呢?這就是我們從這節(jié)課開始探究的內(nèi)容。
學習目標
1、進一步熟悉作函數(shù)圖象的步驟,會畫反比例函數(shù)的圖象;
2、體會函數(shù)的三種表示方法的相互轉換,逐步提高從函數(shù)圖象獲取信息的能力;
3、探索并掌握反比例函數(shù)的主要性質。
反比例函數(shù)圖象的畫法
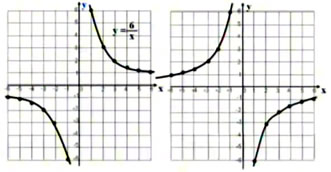
畫出反比例函數(shù)y=6/x和y=-6/x的函數(shù)圖象。
| x |
… |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
6 |
… |
| y=6/x |
… |
-1 |
-1.2 |
-1.5 |
-2 |
-3 |
-6 |
6 |
3 |
2 |
1.5 |
1.2 |
1 |
… |
| y=-6/x |
… |
1 |
1.2 |
1.5 |
2 |
3 |
6 |
-6 |
-3 |
-2 |
-1.5 |
-1.2 |
-1 |
… |
你認為作反比例函數(shù)圖象時應注意哪些問題?
1、列表時,在自變量取值范圍內(nèi)取一些值,并計算相應的函數(shù)值。選取的自變量的值,既要易于計算,又要便于描點,盡量多取一些數(shù)值(取互為相反數(shù)的一對一對的數(shù)),多描一些點,這樣既可以方便連線,又可以使圖象精確。
2、描點時,要嚴格按照表中所列的對應值描點,絕對不能把點的位置描錯。
3、連線時,一定要養(yǎng)成按自變量從小到大的順序依次畫線,連線時必須用光滑的曲線連接各點,不能用折線連接。
4、圖象是延伸的,注意不要畫的有明確端點。
反比例函數(shù)的圖象是由兩支曲線組成的。故稱反比例函數(shù)的圖象為雙曲線。
反比例函數(shù)的圖象在哪兩個象限,是由什么決定的?y隨x的變化有怎樣的變化?
由k的符號決定。
當k>0時,兩支曲線分別位于第一、三象限內(nèi),y隨x的增大而減小;
當k<0時,兩支曲線分別位于第二、四象限內(nèi),y隨x的增大而增大。
歸納:反比例函數(shù)的圖象和性質
1、反比例函數(shù)的圖象是雙曲線。
2、圖象性質見下表:
| y=k/x |
k>0 |
k<0 |
| 圖象 |
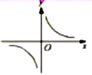 |
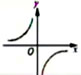 |
| 性質 |
當k>0時,函數(shù)圖象的兩個分支分別在第一、三象限,在每個象限內(nèi),y隨x的增大而減小 |
當k<0時,函數(shù)圖象的兩個分支分別在第二、四象限,在每個象限內(nèi),y隨x的增大而增大 |
跟蹤練習1
1、函數(shù)y=20/x的圖象在第________象限,在每一象限內(nèi),y隨x的增大而______。
2、函數(shù)y=-30/x的圖象在第________象限,在每一象限內(nèi),y隨x的增大而______。
3、函數(shù)y=π/x,當x>0時,圖象在第_____象限,y隨x的增大而______。
跟蹤練習2
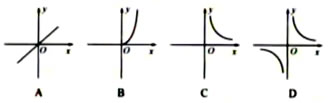
反比例函數(shù)y=-5/x的圖象大致是( )
跟蹤練習3
已知反比例函數(shù)y=(4-k)/x。
(1)若函數(shù)的圖象位于第一、三象限,則k______;
(2)若函數(shù)的圖象位于第二、四象限,則k______。
跟蹤練習4
考察函數(shù)y=2/x的圖象,當x=-2時,y=______;當x<-2時,y的取值范圍是______;當y<-1時,x的取值范圍是______。
跟蹤練習5
甲乙兩地相距100km,一輛汽車從甲地開往乙地,把汽車到達乙地所用的時間y(h)表示為汽車的平均速度x(km/h)的函數(shù),則個函數(shù)的圖象大致是( )
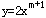 是反比例函數(shù),則m=________。
是反比例函數(shù),則m=________。