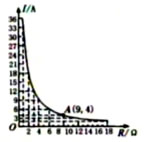
| R/Ω | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| I/A |
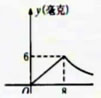
此內容正在抓緊時間編輯中,請耐心等待
張老師
女,中教高級職稱
優秀教師,市級骨干教師、“教學標兵”、勞動模范,市數學教學與研究科研組帶頭人,注重教學改革與實踐。
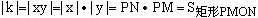




| R/Ω | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| I/A |

此內容正在抓緊時間編輯中,請耐心等待
張老師
女,中教高級職稱
優秀教師,市級骨干教師、“教學標兵”、勞動模范,市數學教學與研究科研組帶頭人,注重教學改革與實踐。

九年級數學下冊第28章《銳角三角函數》28.1 銳角三角函數(1)

九年級數學下冊第27章《相似》27.3 位似(1)

九年級數學下冊第27章《相似》27.2.3 相似三角形應用舉例

九年級數學下冊第27章《相似》27.2.2 相似三角形的性質

九年級數學下冊第27章《相似》27.2.1 相似三角形的判定(3)

九年級數學下冊第27章《相似》27.2.1 相似三角形的判定(2)

九年級數學下冊第27章《相似》27.2.1 相似三角形的判定(1)

九年級數學下冊第27章《相似》27.1 圖形的相似(2)

九年級數學下冊第27章《相似》27.1 圖形的相似(1)
 正在播放
正在播放
九年級數學下冊第26章《反比例函數》26.2 實際問題與反比例函數(2)

九年級數學下冊第26章《反比例函數》26.2 實際問題與反比例函數(1)

九年級數學下冊第26章《反比例函數》26.1.2 反比例函數的圖象與性質(2)

九年級數學下冊第26章《反比例函數》26.1.2 反比例函數的圖象與性質(1)
評論
點此登錄 后即可暢所欲言
[山東省] 老師教導的很好,孩子很愿意學,支持哦

186****9802
2018-11-06 19:28:31
[河北省衡水市] 老師講的很好,孩子很愿意學,支持

shangcuiyan
2016-12-03 09:31:02
[山東省] 非常好非常好!

133****1052
2016-08-09 21:01:24
[山東省] 不錯不錯哦!

133****1052
2016-08-09 20:35:26
[湖南省懷化市] good

1096086059
2016-08-02 10:54:56
[廣東省肇慶市] 很好!

tzjx1968
2016-05-24 07:14:52