【此視頻課程與人教版第15課的知識點相同,同樣適用于魯教版第1課,敬請放心學習。】
課程內容:
《平方差公式》
探究:計算下列多項式的積,你能發現什么規律?
(1)(x+1)(x-1)=________;(2)(m+2)(m-2)=_________;
(3)(2x+1)(2x-1)=_____________。
一般地,我們有 (a+b)(a-b)=a2-b2
即兩個數的和與這兩個數的差的積,等于這兩個數的平方差。這個公式叫做(乘法的)平方差公式。
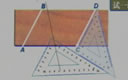
討論:你能根據下圖中的面積說明平方差公式嗎?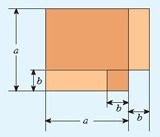
例1:運用平方差公式計算:
(1)(3x+2)(3x-2); (2)(b+2a)(2a-b)
(3)(-x+2y)(-x-2y)
例2.計算:
(1)102×98; (2)(y+2)(y-2)-(y-1)(y+5)
練習:
1.下面各式的計算對不對?如果不對,應當怎樣改正?
(1)(x+2)(x-2)=x2-2;(2)(-3a-2)(3a-2)=9a2-4
2.運用平方差公式計算:
(1)(a+3b)(a-3b); (2)(3+2a)(-3+2a);
(3)51×49; (4)(3x+4)(3x-4)-(2x+3)(3x-2)
思維延伸:
已知兩個正方形的周長之和等于32cm,它們的面積之差為48cm2,求這兩個正方形的邊長。
創新應用:
如圖,在邊長為a的正方形中挖掉一個邊長為b的正方形(a>b)。把余下的部分剪成一個矩形(如圖2),通過計算兩個圖形(陰影部分)的面積,驗證了一個等式,這個等式是( )。
A.a2-b2=(a+b)(a-b) B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2 D.(a+2b)(a-b)=a2+ab-2b2
綜合拓展:
1.計算20042-2003×2005;
2.請你利用平方差公式求出(2+1)(22+1)(24+1)(28+1)…(264+1)的值。
此內容正在抓緊時間編輯中,請耐心等待
尚老師
男,中教高級職稱
長期從事中學數學教學工作,重視學生對知識的理解與運用,市優秀教師、骨干教師,數學學科帶頭人。