課程內容
《相似三角形的判定》
先回顧初中已學的相似三角形知識
定義:對應角相等,對應邊成比例的兩個三角形叫做相似三角形,相似三角形對應邊的比值叫做相似比(或相似系數)
由于從定義出發判斷兩個三角形是否相似,需要考慮6個元素,即三級對應角是否分別相等,三能對應邊是否分別成比例,顯然比較麻煩所以我們曾經給出過如下幾個判定兩個三角形相似的簡單方法。
(1)兩角對應相等,兩三角形相似。
(2)兩邊對應成比例且夾角相等,兩三角形相似。
(3)三邊對應成比例,兩三角形相似。
下面對這些判定方法進行嚴格證明
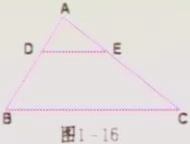
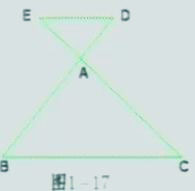
如圖1-16在△ABC中,D分別是AB、AC邊上的點,且DE∥BC由上一節的例3可知,△ADE和△ABC對應邊成比例又由DE∥BC可得,∠ADE=∠B,∠AED=C,而∠A公共角,因此△ADE∽△ABC,探究,如果D、E的延長線上,且DE∥BC(圖1-17)那么結論是否還成立?
對于圖1-17的情形,同樣可以證明△ADE∽ABC這是判定兩個三角形相似的一個定理,我們把它稱為預備定理。
預定定理
平行于三角形一邊的直線和其他兩邊(或兩邊的延長線)相交,所構成的三角形與原三角形相似。
下面從預備定理出發,看看能否得出一些新的結論。
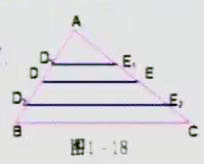
可以發現只要DE∥BC,無論D、E在AB、AC邊上什么位置,都有△ADE∽△ABC,如圖1-18,如果D1E1∥BC(ⅰ=1.2……)那么也有△ABC∽AD1E1(ⅰ=1.2……)從運動變化的觀點過程中,△ADE的邊長改變,南昌角的大小始終不變,這說明,只要兩個三角形的三個對應角相等,那么它們就相似,又由于三角形的內角和為180度,所以只要兩個三角形中有兩個對應角相等,那么第三個對應角一定相等,這樣就有“兩角對應相等,兩三角形相似”。
一般地,我們有
判定定理1 對于任意兩個三角形,如果一個三角開的兩個角與另一個三角形的兩個角對應相等,那么這兩個三角形相似簡述為:兩個角對應相等,兩三角形相似。
已知,如圖1-19,在△ABC和△A'B'C'中,∠A=A',∠B=B'
求證:△ABC∽△A'B'C'
證明:在△ABC的邊AB(或AB的延長線)上,截取AD=A'B',邊D作DE∥BC,交AC于點E,由預備定理得△ADE∽△ABC,
因為∠ADE=∠B,∠B=B',所以∠ADE=B',
又因為∠A =A',AD=A'B',所以△ADE≌△A'B'C',
因此△ABC=△A'B'C'
例1 如圖1-20,在△ABC中,AB=Ac,D是AC邊上一點BD=BC
求證 BC=AC.CD
分析,要證明BC=AC.CD,即證明AC/BC=BC/CD,只要證明AC、BC和BC、CD為一對相似三角形的兩組對應邊,即可為此,要證明△ABC和△BDC相似,
證明,因為△ABC是等腰三角形,所以∠A=180-2∠C,
因為△BCD也是等腰三角形,所以∠=180-2∠C,
則∠A=∠DBC,又因為∠C是公共角,故△ABC∽△BDC,
因此,AC/BC=BC/CD,即BC=AC.CD。
例2 如圖1-21,圓內接△ABC的角平分線CD延長后交圓于點E,求證EB/EC=DB/CB
分析,要證EB/EC=DB/CB,應考慮EB、EC、DB、CB這四條線段所在的兩個三角形是否相似EB、EC在△EBD中,DB、CB在△ECB中,因此可以考慮證明△EBD與△ECB相似
證明:由已知,可得∠ACE=∠BCE,因此∠ACE與∠ABE是同弧上的圓周角,故∠ACE=∠ABE,則∠BCE=∠ABE,
又因為∠BED=∠CEB,故△EBD∽△ECB,因此EB/EC=DB/CB。
判定定理2 對于用意兩個三角形,如果一個三角形的兩邊和一個三角形的兩邊對應成比例,并且夾角相等,那么這兩個三角形相似,簡述為:兩邊對應成比例且夾角相等,兩三角形相似。
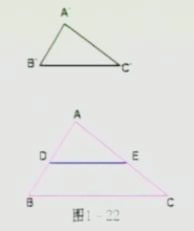
已知:如圖1-22,在△ABC和△A'B'C'中,∠A=A',A'B'/AB=A'C'/AC
求證:△ABC∽△A'B'C'
由平行線分線段成比例定理的推理可知,當DE∥BC時,有AD/AB=AE/AC,因而,我們猜想這個推理的逆命題可能是成立的,這樣,我們需要先證明下面命題
引理 如果殊不知直線截三角形的兩邊(或兩邊的延長線)所得的對應線段成比例,那么,這條直線平行于三角形第三邊。
已知,如圖△ABC中,D、E分別在AB,AC上,且AD/AB=AE/AC
求證:DE∥BC
證明:過D作直線DE∥BC,交AC于點E,則AD/AB=AE/AC(為什么?)
因為AD/AB=AE/AC,所以AE/AC=AE/AC,則AE=AE'。
因此,點E與點E'重合,即直線DE與直線DE重合。所以DE∥BC。
在探究數學問題過程中,應當做到”步步有據“有時,為了尋找某個步驟的推理依據,往往會產生一個原問題的輔助問題,數學家把這種輔助問題稱為引理,顯然,引理的證明為解決問題奠定了基礎。
當直接證明一個問題比較困難時,往往采用間接的方法上述引理的證明采用的“同一法”,就是一種間接證明方法,應用同一法證明問題時,往往先作出一個滿足命題結論的圖形,然后證明符合命題已知條件,確定所作圖形與題設條件所指的圖形相同。
例3,如圖1-24,在△ABC內任取一個點D,連接AD和BD點E在△ABC外,∠EBC=∠ABD=∠DAB
求證:△DBE∽△ABC
證明:在△DBE與△ABC中,∠DBE+∠CBD,∠ABC=∠ABD+∠DBC,因為∠ABD=∠ABD+∠DBC,因為∠ABD=∠EBC,
所以∠DBE=∠ABC……(1)在△ABD與△CBE中,由已知條件有∠EBC=∠ABD=∠DAB,所以△ABD∽△CBE。
則BE/BD=BC/AB,即BE/BC=BD/AB……(2)
綜合(1)(2)式,由判定定理2知△DBE∽△ABC
此內容正在抓緊時間編輯中,請耐心等待
宋老師
女,中教高級職稱
市級重點中學語文教師,高級教師職稱,曾在全省、全國青年教師課堂教學大賽中獲獎,具有豐富的語文教學經驗。















