榴莲视频官网_国产尤物精品视频_在线成年人视频_国产一区二区三区夜色

課程內容

《不等式和絕對值不等式》
這節課我們來研究：絕對值有什么性質？
我們知道，一個實數的絕對值的意義：

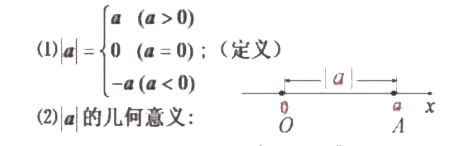
表示數軸上坐標為a的點A到原點O的距離。
關于絕對值還有什么性質呢？
①∣a∣√a²
思考：用恰當的方法要數軸上把∣a∣，∣b∣，∣a+b∣表示出來，你能發現它們之間的什么關系？
注：絕對值的幾何意義：

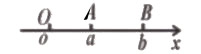
（1）∣a∣表示數軸上的數A對應的點與原點O的距離∣OA∣；
（2）∣a-b∣表示數軸上的數A對應的點與數b對應的點B的距離，如圖：
即∣a∣=∣OA∣，∣a-b∣=∣AB∣
定理1 如果a，b是實數，則∣a+b∣≤∣a∣+∣b∣（當且僅當ab≥0時，等號成立）
（1）若把a，b換為復數z₁，z₂,

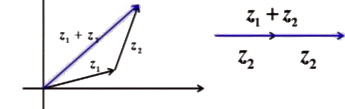
結論：∣z₁+z₂∣≤∣z₁∣+∣z₂∣成立嗎？
（2）若把a，b換為向量（→，a），（→，b）情形又怎樣呢？
∣∣a∣-∣b∣∣≤∣a+b∣≤∣a∣+∣b∣
-b代b，得：∣a∣-∣-b∣≤∣a+（-b）∣≤∣a∣+∣-b∣
即∣∣a∣-∣b∣∣≤∣a-b∣≤∣a∣+∣b∣
定理（絕對值三角不等式）
如果a，b，是實數，則∣∣a∣-∣b∣∣≤∣a±b∣≤∣a∣+∣b∣
注：當a、b為復數或向量時結論也成立。
注意：1°這個不等式俗稱“三角不等式”——三角形中兩邊之和大于第三邊，兩邊之差小于第三邊
2°，對于∣∣a∣-∣b∣∣≤∣a-b∣≤∣a∣+∣b∣
a，同號時右邊取“=”，a，b異號時左邊取“=”
3°，對于∣∣a∣-∣b∣∣≤∣a-b∣≤∣a∣+∣b∣
a，同號時左邊取“=”，a，b異號時右邊取“=”
我們還可討論涉及多個實數的絕對值不等式的問題：
推論1 （運用數學歸納法可得）：
∣a₁+a₂+…+a_n∣≤∣a₁∣+∣a₂∣+…+∣a_n∣.
定理2：如果a、b、c是實數，那么∣a-b∣≤∣+a-b∣+∣b-c∣,
當且僅當（a-b）（b-c）≥0時，等號成立。
例題
例1 已知ε﹥0，∣x-a∣＜ε,∣y-b∣＜ε，
求∣2x+3y-2a-3b∣＜5ε
例2 已知∣x-a∣＜ε/2M，0＜∣y-b∣＜ε/2∣a∣,y∈（0，M）,
求證∣xy-ab∣＜ε。 
練習
1.①已知∣x∣﹥r﹥0，a≠0，求證∣1/ax∣＜1/∣a∣r。
  ②已知∣a_n-ι∣＜1,求證∣a_n∣＜∣ι∣ +1。
2.已知∣A-a∣＜ε/2，∣B-b∣＜ε/2,求證：
①∣（A+B）-（a+b）∣＜ε；
②∣（A-B）-（a-b）∣＜ε。
例2 兩個施工隊分別被安排在公路沿線的兩個地點施工，這兩個地點分別位于公路碑的第10公里和第20公里處，現要在公路沿線建兩個施工隊的共同臨時生活區，每個施工隊每天在生活區和施工地點之間往返一次，要使兩個施工隊每天往返的路程之和最小，生活區應該建于何處？
解：如果生活區建于公路碑的第xkm處，兩施工隊每天往返的路程之和為s（x）km
那么 S（x）=2（∣x-10∣+∣x-20∣）,要求問題化歸為求該函數的最小值，可用絕對值三角不等式求解。
小結：理解和掌握絕對值不等式的兩個定理：
如果a，b，是實數，則∣∣a∣-∣b∣∣≤∣a±b∣≤∣a∣+∣b∣
注：當a、b為復數或向量時結論也成立。
定理2：如果a、b、c是實數，那么∣a-b∣≤∣+a-b∣+∣b-c∣,
當且僅當（a-b）（b-c）≥0時，等號成立。