榴莲视频官网_国产尤物精品视频_在线成年人视频_国产一区二区三区夜色

課程內容

《用關系式表示變量之間的關系》
學習目標
1、能根據具體情況，用關系式表示某些變量之間的關系。
2、根據關系式求值，體會自變量和因變量的數值對應關系。
問題探究
1、操作演示
2、思考
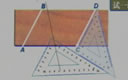
（1）如果△ABC底邊BC上的高是6厘米。當三角形的頂點C沿底邊BC所在直線上運動時，三角形的面積發生了怎樣的變化？
（2）這個變化過程中，自變量、因變量各是什么？
（3）如果三角形的底邊長為x（厘米），那么三角形的面積y（厘米²）可以表示為__________。
3、體會、探究
（1）體會：根據三角形的底邊長x（厘米）和三角形的面積y（厘米²）的關系式填表。
（2）歸納、探究：當底邊長從12厘米變化到3厘米時，三角形的面積從36平方厘米變化到9平方厘米。
4、歸納、總結
（1）通過觀察變動三角形的多媒體動畫，體會到因變量（三角形的面積）是隨自變量（三角形的底邊長）變化而變化。
（2）關系式可以表達變量間的關系，在運用關系式由自變量取值求因變量的值的過程中體會到用關系式表達變量間的關系的優勢。
（3）操作機器圖的過程中體會到“關系式”好比數字處理器。
變式探究
問題一：如圖所示，圓錐的底面半徑是2厘米，當圓錐的高由小到大變化時，圓錐的體積也隨之而發生了變化。
（1）在這個變化過程中，自變量是_______，因變量是_______。
（2）如果圓錐的高為h（厘米），那么圓錐的體積V（厘米³）與h的關系式是_______。
（3）當高由1厘米變化到10厘米時，圓錐的體積由_______厘米³變化到_______厘米³。
問題二：如圖所示，圓錐的高是4厘米，當圓錐的底面半徑由小到大變化時，圓錐的體積也隨之而發生了變化。
（1）在這個變化過程中，自變量是_______，因變量是_______。
（2）如果圓錐底面半徑為r（厘米），那么圓錐的體積V（厘米³）與r的關系式是_______。
（3）當底面半徑由1厘米變化到10厘米時，圓錐的體積由_______厘米³變化到_______厘米³。
嘗試、鞏固
在地球某地溫度T（℃）與高度d（m）的關系可以近似的用T=10-d/150來表示。根據這個關系式，當d的值分別是0、200、400、600、800、1000時，計算相應的T值，并用表格表示所得結果。
合作探究
如圖所示，梯形上底的長是x，下底的長是15，高是8。
（1）梯形面積y與上底長x之間的關系式是什么？
（2）用表格表示當x從10變到20時（每次增加1），y的相應值。
（3）當x每增加1時，y如何變化？說說你的理由。
（4）當x=0時，y等于什么？此時它表示的什么？
方法深化
我是一名初一學生，我的身高是160cm，在植樹節那天種子一株高為40cm的樹苗，栽種后每周樹苗約長高15cm，多久以后樹苗會超過我的身高？
小結反思
通過本節課的學習，你學到了什么？有什么收獲？
1、可以用關系式表示某些變化的量。
2、根據關系式求值。