【此視頻課程與人教版第15課的知識(shí)點(diǎn)相同,同樣適用于華師大第13課,敬請(qǐng)放心學(xué)習(xí)。】
課程內(nèi)容:
《因式分解(公式法)》
回顧:平方差公式
兩個(gè)數(shù)的和與兩個(gè)數(shù)的差的積等于這兩個(gè)數(shù)的平方差:
(a+b)(a-b)=a2-b2
反過來可以得到:a2-b2=(a+b)(a-b)
例1.把下列各式分解因式:
(1)25-16x2; (2)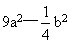
練一練:把下列各式進(jìn)行因式分解
(1)a2-81; (2)36-x2; (3)1-16b2; (4)m2-9n2;
(5)0.25q2-121p2; (6)169x2-4y2;
(7)9a2p2-b2q2; (8)-16x2+81y2。
想一想:以前學(xué)過兩個(gè)乘法公式:
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
把兩個(gè)公式反過來就得到:
a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2
形如上列的式子稱為完全平方式。由分解因式與整式乘法的關(guān)系可以看出,如果把乘法公式反過來,那么就可以把某些多項(xiàng)式分解因式。這種分解因式的方法叫做運(yùn)用公式法。
例2.判斷下列各式是不是完全平方式,并說說理由。
(1)a2+4a+4; (2)x2+4x+4y2;
(3)x2-6x-9; (4)a2-ab+b2;
(5)4a2+2ab+b2/4; (6)(a+b)2+2(a+b)+1
例3.下列各多項(xiàng)式是不是完全平方公式?若是,請(qǐng)找出相應(yīng)的a和b。
(1)x2+12x+36; (2)-2xy+x2+y2;
(3)-2xy-x2+y2; (4)m2/4+3mn+9m2;
(5)(a+b)2-6(a+b)+9
例4.把以下兩個(gè)多項(xiàng)式分解因式。
(1)x2+12x+36 (2)-2xy+x2+y2 (3)(a+b)2-6(a+b)+9
思考討論:分解因式
(1)3am2+3an2+6amn (2)-a2-4b2+4ab
小結(jié):
本節(jié)課主要學(xué)習(xí)了兩種分解因式的方法,平方差公式和完全平方公式逆向得出用公式法分解因式的方法和過程。
此內(nèi)容正在抓緊時(shí)間編輯中,請(qǐng)耐心等待
尚老師
男,中教高級(jí)職稱
長期從事中學(xué)數(shù)學(xué)教學(xué)工作,重視學(xué)生對(duì)知識(shí)的理解與運(yùn)用,市優(yōu)秀教師、骨干教師,數(shù)學(xué)學(xué)科帶頭人。