【此視頻課程與人教版第15課的知識點相同,同樣適用于華師大第13課,敬請放心學習。】
課程內容:
《因式分解復習》
一、知識點整理
概念 方法 步驟 應用
方法:①提取公因式法;②運用公式法;③十字相乘法;④分組分解法
步驟:一、提 二、套 三、十字 四、分組 五、查
三.分解因式過程中應注意的幾個問題:
(1)分解因式總是在指定的數集中進行,不作特別的說明,一般指實數范圍內進行;
(2)分解因式的結果是幾個整式積的形式,而每一個因式都應分解到不能分解為止;
(3)在提取公因式時,要防止出現提取不盡、提取全項后,得該項為零、提取系數為負的因式疏忽變號等錯誤;
(4)運用公式法應當注意,當平方項不是一個字母或數時,可用“換元法”進行分解因式。
因式分解公式:
ma+mb+mc=m(a+b+c)
a2-b2=(a+b)(a-b)
a2±2ab+b2=(a±b)2
x2+(p+q)x+pq=(x+p)(x+q)
練習:
1.下列由左到右的變形是因式分解的是( )
A.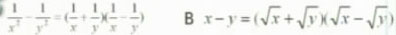
C.(3x+y)(3x-y)=9x2-y2 D.4x2-1=(2x+1)(2x-1)
2.下列因式分解正確的是:( )
A.ab-a-b+1=(a-1)(b-1) B.a4-b2=(a2+b)(a2-b)
C.x2-3x-4=(x+2)(x-2) D.3x3+2x2+x=x(3x2+2x)
算一算:
1.分解因式
(1)-x2-2x; (2)ax2+4ay2+4axy; (3)a2(x-y)+(y-x)3;
(4)4x2-y2-2y-1; (5)3x2-4√3x+3
2.(1)20052-2005×2006=
(2)
3.若m-n=6,mn=7,則mn2-m2n的值是_____________________。
若x2+xy=2,y2+xy=7,則x2-y2=____________________。
4.已知正整數x、y滿足x2-12=y2,則x+y的值是_______________。
四、因式分解的應用
1.觀察圖形,根據圖形的面積關系,不需要其他的線,便可以得到一個用來分解因式的公式,這個公式是______________________________。
2.在邊長為a的正方形中挖掉一個邊長為b的小正方形,把余下的部分剪拼成一個矩形,通過計算這兩個圖形的面積,驗證了一個等式,則這個等式是( )
A.a2-b2=(a+b)(a-b) B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2 D.(a+2b)(a-b)=a2+ab-2b2
3.如圖,用4張全等的矩形紙片拼成的圖形,請利用圖中空白部分的面積的不同表示方法寫出一個關于a、b的恒等式。
4.閱讀下面因式分解的過程,再回答所提出的問題:
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x)=(1+x)3
(1)上述分解因式的方法是____________,共應用了________次;
(2)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2005,則應用上述方法____________次,結果是___________________;
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+x(x+1)n(n為正整數)。
6.請你給代數式x2+4加上一個單項式后,使它能成為一個整式的平方,請你寫出所有符合條件的單項式。
7.請寫出一個三項式,使它能先提取公因式,再運用公式法來分解,你編寫的三項式是_______________,分解因式的結果是_____
此內容正在抓緊時間編輯中,請耐心等待
尚老師
男,中教高級職稱
長期從事中學數學教學工作,重視學生對知識的理解與運用,市優秀教師、骨干教師,數學學科帶頭人。