榴莲视频官网_国产尤物精品视频_在线成年人视频_国产一区二区三区夜色

課程內容
《拋物線的簡單幾何性質》
一、復習回顧
1、拋物線的定義
動點M與一個定點F的距離和它到一條直線L的距離的比是常數e=1，則這個點的軌跡是拋物線。
定點F是拋物線的焦點；
定直線L叫做拋物線的準線；
常數e=1拋物線的離心率。
y2=2Px  P﹥0是焦準距
拋物線標準方程
2、拋物線的標準方程

標準方程	y2=Px(p﹥0)	y2=-Px(P﹥0)	x2=2Py(P﹥0)	x2=-2Py(P﹥0)
圖形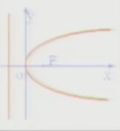
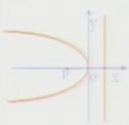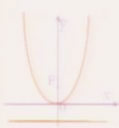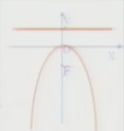焦點	F（P/2，0）	F（-P/2，0）	F（0，P/2）	F（-0，P/2）
準線	x=-P/2	x=P/2	y=-P/2	y=P/2

3、橢圓和雙曲線的性質：

性質  方程	x2/a2+y2/b2=I(a﹥b﹥0)	x2/a2-y2/b2=I(a﹥0，b﹥0)
圖形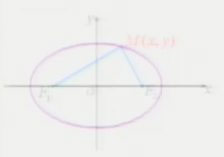
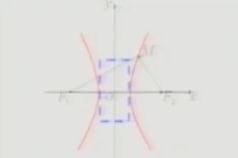范圍	-a≤x≤a,-b≤v≤b	x≤-a或x≥a,y ∈R
對稱性	關于Xx，y軸用原點對稱	關于x，y軸及原點對稱
頂點坐標	A1（-a，0），A2（a，0） B1（0，-b），B2（0，b） A1A2叫長軸B1B2叫短軸	A1（-a，0），A2（a，0）  A1A2叫實軸B1B2叫虛軸
離心率	e=e/a，（0＜e＜1）	e=e/a，（e﹥1）

二、講授新課
以拋物線的標準方程y²=2P經（P﹥0）來研究它的幾何性質。
（1）范圍
因為P﹥0，由方程可知x≥0，所以拋物線在y軸的右側，當x的值增大時∣y∣也增大，這說明拋物線向右上方和右下方無限延伸。
（2）對稱性
以-y代y，方程不變，所以拋物線關于x對稱，我們把拋物線的對稱軸叫做拋物線的軸。
（3）頂點
拋物線與它的軸的交點叫做拋物線的頂點，在方程中，當y=0時，x=0，因此拋物線的頂點就是坐標原點。
（4）離心率
拋物線上的點與焦點的距離和它互準線的距離的比，叫做拋物線的離心率，由拋物線的定義可知e=1。
根據上表中拋物線的標準方程的不同形式與圖形，焦點坐標，準線方程對應關系如何判斷拋物線的焦點位置，開口方向？
第一：一次項的變量如為X（或Y），則X軸（或Y軸）為拋物線的對稱軸，焦點就在對稱軸上！
第二：一次項的系數決定了開口方向。
特點：
1、拋物線只位于送修坐標平面內，雖然它可以無限延伸，但它沒有漸近線；
2、拋物線只有一條對稱軸，沒有對稱中心；
3、拋物線只有一個頂點，一個焦點，一條準線；
4、拋物線的離心率是確定的e=1；
5、拋物線的標準方程中的P對拋物線開口的影響。
P越大，開口越開闊——本質是成比例地放大！
三、例題選講
例1，頂點在坐標原點，對稱軸是坐標軸，并且過點M（2，-2√2）的拋物線有幾條，求它的標準方程。
當焦點在x（或y）軸上，開口方向不定時，設為y²=mxz（m≠0）{或x²=my(m≠0)}，可避免討論。
例2，（1）過拋物線y²=8x的焦點，作傾斜角為45度的直線，則被拋物線截得的弦長為（   ）。
（2）過拋物線的焦點做傾斜角為Q的直角線L，設L交拋物線于A,B兩點，（1）求∣AB∣；（2）求∣AB∣的最小值。
思考：通徑是拋物線的焦點弦中最短的弦嗎？
例3、過拋物線焦點作直線交拋物線y²=2Px(P﹥0)于A，B兩點，判斷與AB為直徑的圓準線的位置關系。