課程內容
《圖形的旋轉》
1、什么是圖形的旋轉?
旋轉的定義:在平面內,將一個圖形繞一個定點按某個方向轉動一定的角度,這樣的圖形運動叫做圖形的旋轉。這個定點叫做旋轉中心,轉動的角度叫做旋轉角。
2、旋轉前后,圖形的形狀、大小、位置是否發(fā)生變化?旋轉變換有什么特征?
操作1、將三角板ABC繞點C按逆時針方向旋轉到DEC的位置,旋轉前、后三角形的位置改變了嗎?形狀、大小改變了嗎?
度量∠ACD與∠BCE的度數(shù),線段AC與DC、BC與EC的長度,你發(fā)現(xiàn)了什么?
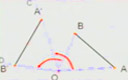
操作2:將△ABC繞點O按順時針方向旋轉到△A′B′C′的位置,度量∠AOA′、∠BOB′與∠COC′的度數(shù),線段AO與A′O、BO與B′O、CO與C′O的長度,你發(fā)現(xiàn)了什么?
旋轉前、后的圖形全等。對應點到旋轉中心的距離相等;每一對對應點與旋轉中心的連線所成的角彼此相等。
考考你
1、已知線段AB和點O,畫出AB繞點O逆時針旋轉100°后的圖形。
小結:如何按要求作出簡單平面圖形旋轉后的圖形?
作圖的步驟:
(1)確定旋轉中心、旋轉方向和旋轉角。
(2)在已知圖形上找一些關鍵點
(3)作出這些關鍵點的對應點
(4)順次連接這些對應點
作圖關鍵:旋轉中心、旋轉方向、旋轉角度、旋轉的對應點。
2、如圖,畫出△ABC繞點C按順時針方向旋轉120°后的對應的三角形。
3、香港特別行政區(qū)區(qū)旗中央的紫荊花圖案由5個相同的花瓣組成,它是由其中一個瓣經過幾次旋轉得到的?
紫荊花圖案繞中心旋轉多少度后能和原來的圖案互相重合?
例題講解
例題1:如圖,E是正方形ABCD中CD邊上任意一點,以點A為中心,把△ADE順時針旋轉90°,畫出旋轉后的圖形。
變式:如圖,正方形ABCD中,E是CD邊上任意一點,將三角形ADE順時針旋轉,得到三角形ABF。
(1)旋轉中心是哪一點?
(2)旋轉了多少度?
(3)點M是AD的中點,經上述旋轉后,點M到什么位置?
(4)連結EF,△AEF是什么三角形?
(5)若正方形ABCD的邊長是2,
①則點M在旋轉時經過的路徑長是多少?
②求四邊形AFCE的面積。
課堂小結
這節(jié)課,主要學習了什么?
1、確定一個圖形旋轉后的位置的條件:
(1)圖形原來的位置
(2)旋轉中心
(3)旋轉方向和旋轉角
2、利用旋轉的基本性質作出簡單平面圖形旋轉后的圖形。
此內容正在抓緊時間編輯中,請耐心等待
馬老師
女,中教高級職稱
從教30年,數(shù)學教研組長,市級骨干教師。曾在全國青年教師課堂教學大賽中獲獎,具有豐富的數(shù)學教學經驗。