榴莲视频官网_国产尤物精品视频_在线成年人视频_国产一区二区三区夜色

課程內容：

《矩形、菱形、正方形（3）》
定義：有一組鄰邊相等且有一個角是直角的平行四邊形叫做正方形。
由正方形的定義可知：正方形既是有一組鄰邊相等的矩形，又是有一個角為直角的菱形。
正方形性質：邊——對邊平行；四邊相等；角——四個角都是直角；對角線——對角線相等；對角線互相垂直；對角線互相平分；每條對角線平分一組對角；對稱性——正方形是軸對稱圖形，也是中心對稱圖形。
例1.求證：正方形的兩條對角線把正方形分成四個全等的等腰直角三角形。
證明：已知：四邊形ABCD是正方形。求證：△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形。
例2.如圖，正方形ABCD中，AC、BD相交于O，MN∥AB且MN分別交OA、OB于M、N。求證：BM=CN。
選擇題：
1.正方形具有而菱形不一定具有的性質是（  ）
    A.對角線互相垂直  B.對角線互相平分  C.對角線相等  D.對角線平分一組對角
2.從四邊形內能找到一點，使該點到各邊距離都相等的圖形可能是（  ）
    A.平行四邊形、矩形、菱形    B.菱形、矩形、正方形
    C.矩形、正方形              D.菱形、正方形
3.下列判斷中正確的是（  ）
    A.四邊相等的四邊形是正方形    B.四角相等的四邊形是正方形
    C.對角線垂直的平行四邊形是正方形    D.對角線互相垂直平分且相等的四邊形是正方形
4.在四邊形ABCD中，點O是對角線的交點，能判定這個四邊形是正方形的是（  ）
    A.AC=BD,AB∥CD,AB=CD      B.AD∥BC,∠A=∠C
    C.AO=BO=CO=DO,AC⊥BD      D.AO=CO,BO=DO,AB=BC
填空：3.已知正方形的一條邊長為4cm，則這個正方形的周長為_________，對角線長為___________，面積為____________。
4.已知正方形的一條對角線長為4cm，則它的邊長為__________，面積為___________。
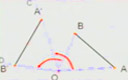
5.已知正方形ABCD中，對角線AC=20cm，P為AD上任意一點，PE⊥AC，PF⊥BD，E、F為垂足，則PE+PF=_____________。
例3.已知：如圖，在正方形ABCD中，F為CD延長線上一點，CE⊥AF于E，交AD于M。求證：∠MFD=45°。