課程內容:
《用反比例函數解決問題(1)》
思考:你吃過拉面嗎?你知道做拉面的過程中滲透著數學知識嗎?體積為20cm3的面團做成拉面,面條的總長度y與面條粗細(橫截面積)s有怎樣的函數關系?
例1.市煤氣公司要在地下修建一個容積為104m3的圓柱形煤氣儲存室。
(1)儲存室的底面積S(單位:㎡)與其深度d(單位:m)有怎樣的函數關系?
(2)公司決定把儲存室的底面積S定為500㎡,施工隊施工時應該向下掘進多深?
(3)當施工隊按(2)中的計劃掘進到地下15m時,碰上了堅硬的巖石。為了節約建設資金,儲存室的底面積應改為多少才能滿足需要(保留兩位小數)?
例2.碼頭工人以每天30噸的速度往一艘輪船上裝載貨物,把輪船裝載完畢恰好用了8天時間。
(1)輪船到達目的地后開始卸貨,卸貨速度v(單位:噸/天)與卸貨時間t(單位:天)之間有怎樣的函數關系?
(2)由于遇到緊急情況,船上的貨物必須在不超過5日內卸載完畢,那么平均每天至少要卸多少噸貨物?
做一做:已知矩形的面積為24,則它的長y與寬x之間的關系用圖象大致可表示為( )
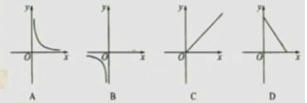
上題中,當矩形的長為12時,寬為_______,當矩形的寬為4,其長為_______。如果要使矩形的長不小于8,其寬至多要_________。
練習:1.有一面積為60的梯形,其上底長是下底長的三分之一,若下底長為x,高為y,則y與x的函數關系是______________。
2.小明家用購電卡買了1000度電,那么這些電能夠使用的天數y與平均每天用電度數x之間的函數關系式是_______________,如果平均每天用5度,這些電可以用________天,如果這些電想用250天,那么平均每天用電__________度。
3.如圖,某玻璃器皿公司要制造一種容積為1升(1升=1立方分米)的圓錐形漏斗。
(1)漏斗口的面積S與漏斗的深d有怎樣的函數關系?
(2)如果漏斗口的面積為100cm2,則漏斗的深為多少?
此內容正在抓緊時間編輯中,請耐心等待
王老師
女,中教高級職稱
省優秀教師,模范共產黨員,學校先進工作者。在教數學的同時,她也是和同學們一起學數學,一起用數學。