| 次數 | 1 | 2 | 3 | 4 | 5 | ... | |
| 紙片數 | 4 | 7 | 10 | 13 | 16 | ... |

| x | 1 | 2 | 3 |
| 2x-2 | 0 0 | 2 2 | 4 4 |
| x+1 | 2 2 | 3 3 | 4 4 |
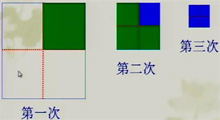
| 估計x的值 | 左邊 | 與右邊64比較 | |
| 第一次估算 | 10 | 31 | 小 |
| 第二次估算 | 20 | 61 | 小 |
| 第三次估算 | 21 | 64 | = |
此內容正在抓緊時間編輯中,請耐心等待
張老師
女,中教高級職稱
優秀教師,市級骨干教師、“教學標兵”、勞動模范,市數學教學與研究科研組帶頭人,注重教學改革與實踐。

| 次數 | 1 | 2 | 3 | 4 | 5 | ... | |
| 紙片數 | 4 | 7 | 10 | 13 | 16 | ... |

| x | 1 | 2 | 3 |
| 2x-2 | 0 0 | 2 2 | 4 4 |
| x+1 | 2 2 | 3 3 | 4 4 |
| 估計x的值 | 左邊 | 與右邊64比較 | |
| 第一次估算 | 10 | 31 | 小 |
| 第二次估算 | 20 | 61 | 小 |
| 第三次估算 | 21 | 64 | = |
此內容正在抓緊時間編輯中,請耐心等待
張老師
女,中教高級職稱
優秀教師,市級骨干教師、“教學標兵”、勞動模范,市數學教學與研究科研組帶頭人,注重教學改革與實踐。

七年級數學上冊第7章《一元一次方程》7.4 一元一次方程的應用(第五課時)

七年級數學上冊第7章《一元一次方程》7.4 一元一次方程的應用(第四課時)

七年級數學上冊第6章《整式的加減》回顧與總結(1)

七年級數學上冊第6章《整式的加減》6.4 整式的加減(2)

七年級數學上冊第6章《整式的加減》6.3 去括號(2)

七年級數學上冊第5章《代數式與函數的初步認識》回顧與總結

七年級數學上冊第7章《一元一次方程》7.4 一元一次方程的應用(1)

七年級數學上冊第7章《一元一次方程》7.3 一元一次方程的解法(第二課時)

七年級數學上冊第7章《一元一次方程》7.3 一元一次方程的解法(第一課時)
 正在播放
正在播放
七年級數學上冊第7章《一元一次方程》7.2 一元一次方程

七年級數學上冊第7章《一元一次方程》7.4 一元一次方程的應用(3)

七年級數學上冊第7章《一元一次方程》7.4 一元一次方程的應用(2)

七年級數學上冊第6章《整式的加減》回顧與總結(2)

七年級數學上冊第2章《有理數》2.3 相反數與絕對值(2)

七年級數學上冊第1章《基本的幾何圖形》回顧與總結

七年級數學上冊第6章《整式的加減》6.2 同類項(2)

七年級數學上冊第6章《整式的加減》6.2 同類項(1)
七年級數學上冊第6章《整式的加減》6.1 單項式與多項式

七年級數學上冊第4章《數據的收集、整理與描述》4.4 扇形統計圖(第二課時)

七年級數學上冊第7章《一元一次方程》7.1 等式的基本性質
評論
點此登錄 后即可暢所欲言