課程內容:
7.5 平行線的性質(第一課時)
一:知識回顧
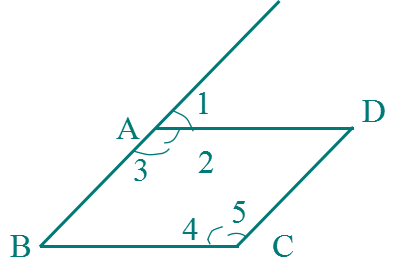
1.如果∠B=∠1,根據_同位角相等,兩直線平行 _ 可得AD//BC
2.如果∠1=∠D,根據__內錯角相等,兩直線平行_ 可得AB//CD
3.如果∠B+∠BCD=180?,根據__同旁內角互補,兩直線平行 可得___AB // CD_
4.如果∠2=∠4,根據____內錯角相等,兩直線平行_ 可得___AD // BC__
5.如果_∠3__=_∠5_,根據內錯角相等,兩直線平行,可得AB//CD
二:大家談談:

如圖7-5-1已知a//b,且他們被第三條直線c所截,由平行線性質定理,可得∠1=∠5.
(1)由∠1=∠5.能推出∠1與∠7相等嗎? ∠2與∠8也相等嗎?為什么?
(2)由∠1=∠5.能推出兩對同旁內角互補嗎?為什么?
三:本節結論:
兩直線平行,同位角相等。
兩直線平行,內錯角相等。
兩直線平行,同旁內角互補。
三:例1 例1 已知:如圖7-5-4,a∥b,c∥d, ∠1=73°.求∠2和∠3的度數.

解:∵a∥b (已知)
∴ ∠2=∠3(兩直線平行,內錯角相等)
∵ ∠1=73°(已知)
∴ ∠2=73°(等量代換)
∵c∥d (已知)
∴ ∠2+∠3=180°(兩直線平行,同旁內角互補)
∴ ∠3=180°-∠2 (等式的性質)
∴ ∠3=180°-73°=107°(等量代換)
此內容正在抓緊時間編輯中,請耐心等待
張老師
女,中教高級職稱
優秀教師,市級骨干教師、“教學標兵”、勞動模范,市數學教學與研究科研組帶頭人,注重教學改革與實踐。