榴莲视频官网_国产尤物精品视频_在线成年人视频_国产一区二区三区夜色

課程內容

《二次函數y=ax²+bx+c的性質》
一、知識回顧及創新思維

二、實踐與探索
（一）二次函數的性質的復習
例1（2009南充）拋物線y=a(x+1)(x-3)(a≠0)的對稱軸是直線(  )
A x=1  B x=-1  C x=-3  D x=1
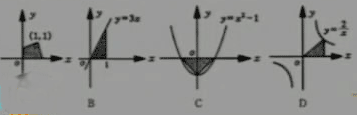
例2 下列圖中陰影部分的面積與算式|3/4|+(1/2)2+2⁴的結果相同的是(  )

例3 （2009湖州）已知拋物線y=ax²+bx+c(a＞0)的對稱軸為直線x=1,且經過點（-1，y）、（2，y₂）,試比較y₁和y₂的大小；y_¹______y_²
例4 已知函數y=x²-（m-2）x+m的圖像過電（-1,15），設其圖像與x軸交于點A,B,點C在圖像上，且S△ABC=1,求點C的坐標。
（二）a、b、c的符號問題
根據我們以前的學習，我們知道a的正負決定二次函數的開口方向，a，b的符號綜合到一起，決定二次函數的對稱軸是在y軸的左側還是右側，c的符號決定著二次函數與y軸交點是在y軸的正半軸還是負半軸。繁殖，由二次函數的圖像也可推出a,b,c的符號。
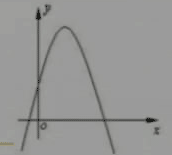
例1 二次函數y=ax²+bx+c（a≠0）的圖像如圖所示，則下列結論：
①a＞0  ②c＞0  ③b2-4ac＞0 ，其中正確的個數是(   )
A 0個   B  1個  C 2個   D 3個

例2 二次函數y-ax²+bx+c（a≠0）的圖像如圖所示，那么abc,b²-4ac,2a+b,4a-2b+c這四個代數式中，值為正的有（   ）
A 4個  B 3個  C 2個  D 1個
例3 二次函數y-ax²+bx+c（a≠0）的圖像如圖所示，則下列結論
①abc＜0；②4ac＜b² ③ 4a-2b+c<0; ④ 2a+b<0
A 2個  B 3個  C 4個  D 5個