課程內容
《二次函數的應用(三)》
一、創設問題情境
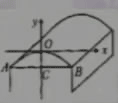
如圖,某建筑的屋頂設計成橫截面為拋物線型(曲線AOB)的薄殼屋頂,它的拱寬AB為4m,拱高CO為0.8m,施工前要先制造建筑模板,怎樣畫出模板的輪廓板呢?
二、引申拓展
問題1:能不能以A為原點,AB所在直線為x軸,過點A的x軸的垂線為y軸,建立直角坐標系?
建立直角坐標系的方法不是唯一的,以A點位原點,AB所在的直線為x軸,過點A的x軸的垂線為y軸,建立直角坐標系也是可行的。
問題2 ,若以A點位原點,AB所在直線為x軸,過點A的x軸的垂直為y軸,建立直角坐標系,你能求出其函數關系式嗎?
三、例題解析
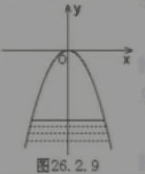
例1 某涵洞時拋物線形,它的界面如圖所示,現測得水面寬1.6m。涵洞頂點O到水面的距離為2.4m。在圖中直角坐標系內,涵洞所在拋物線的函數關系式是什么?
四、練習
1、一個涵洞成拋物線形,它的截面如圖,現測得,當水面寬AB=1.6m時,涵洞頂點與水面的距離為2.4m。這時,離開水面1.5m處,涵洞寬ED是多少?
2、河北省趙縣的趙州橋的橋拱是拋物線型,建立如圖所示的坐標系,其中函數的解析式為y=-(1/25)x2,當水位線在AB位置時,水面寬AB=30米,這時水面離橋頂的高度h是( )
A、5米 B、6米 C、8米 D、9米
3、一座拋物線型拱橋如圖所示,橋下水面寬度是4m,拱高是2m。當水面下降1m后,水面的寬度是多少?(結果精確到0.1m)
此內容正在抓緊時間編輯中,請耐心等待
楊老師
男,中教中級職稱
從教20余年,市優秀教師、“教學標兵”,曾在全省、全國青年教師課堂教學大賽中獲獎。






















