課程內容
《不等關系與不等式（2）》
一、復習回顧
1、用不等式或不等式組表示不等關系
2、a＞b←→a-b＞0
a=b←→a-b=0
a＜b←→a-b＜0
3、比較兩個數或代數式的大小——作差比較法
作差→變形→判斷符號→得出結論
二、不等式的性質
性質1：如果a＞b，那么b＜a；如果b＜a，那么a＞b。
性質1表明：把不等式的左邊和右邊交換位置，所得不等式與原不等式異向，我們把這種性質稱為不等式的對稱性。
性質2：如果a＞b，b＞c，那么a＞c。
這個性質也可以表示為c＜b，b＜a，則c＜a。這個性質是不等式的傳遞性。
性質3：如果a＞b，則a+c＞b+c。
性質3表明，不等式的兩邊都加上同一個實數，所得的不等式與原不等式同向。
a+b＞c→a+b+（-b）＞c→a＞c-b
結論：不等式中的任何一項都可以改變符號后移到不等式另一邊（移項法則）。
性質4：如果a＞b，c＞0，則ac＞bc；如果a＞b，c＜0，則ac＜bc。（可乘性）
性質5：如果a＞b，c＞d，則a+c＞b+d。（加法性質）
幾個同向不等式的兩邊分別相加，所得的不等式與原不等式同向。
性質6：如果a＞b＞0，c＞d＞0，則ac＞bd。（乘法性質）
幾個兩邊都是正數的同向不等式的兩邊分別相乘，所得的不等式與原不等式同向。
性質7：如果a＞b＞0，那么an＞bn，（n∈N，n≥2）（乘方法則）
性質7說明，當不等式兩邊都是正數時，不等式兩邊同時乘方所得的不等式和原不等式同號。
性質8：如果a＞b＞0，那么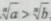
，（n∈N，n≥2）
性質8說明，當不等式的兩邊都是正數時，不等式兩邊同時開方所得不等式與原不等式同向。
性質7、8可歸納為：a＞b＞0 ←→ an＞bn，（n∈R，n＞0）
性質9：a＞b，ab＞0 → 1/a＜1/b（倒數法則）
以上這些關于不等式的事實和性質是解決不等式問題的基本依據。
三、應用
例1：對于實數a，b，c，判斷下列命題的真假
（1）若a＞b則ac2＞bc2
（2）若ac2＞bc2則a＞b
（3）若a＜b＜0則1/a＜1/b
（4）若a＜b＜0則b/a＜a/b
（5）若a＜b＜0則a2＞ab＞b2
例2：已知a＞b＞0，c＜0，求證c/a＞c/b。
例3：應用不等式的性質，證明下列不等式。
已知a＞b＞0，0＜c＜d，求證a/c＞b/d。
例4：a＞b＞0，c＜d＜0，e＜0，則e/（a-c）＞e/（b-d）。
例5：（1）如果30＜x＜36，2＜y＜6，求x-2y及x/y的取值范圍。
（2）若-3＜a＜b＜1，-2＜c＜-1，求（a-b）c2的取值范圍。
此內容正在抓緊時間編輯中，請耐心等待
楊老師
女，中教高級職稱
教學功底扎實，教學經驗豐富，對知識體系有深厚的了解。
