課程內容
《基本不等式√ab≤(a+b)/2(1)》
經“風車”抽象成左圖。在正方形ABCD中有4個全等的直角三角形。令直角三角形兩條直角邊的長為a、b。
S△DGC=1/2ab,即4個直角三角形的面積和為2ab,正方形的面積為a2+b2。
由此得:一般地,對于任意實數a、b,我們有a2+b2≥2ab,當且僅當a=b時,等號成立。
一、不等式(1)a2+b2≥2ab
還有其他的方法證明嗎?
如果a>0,b>0,我們用√a,√b分別代替a、b,可得a+b≥2√ab
通常我們把上式寫作:√ab≤(a+b)/2(a>0,b>0)
二、基本不等式或不等式(2)
√ab≤(a+b)/2(a>0,b>0)或者(a+b)/2≥√ab(a>0,b>0)
當且僅當a=b時,(a+b)/2=√ab
1、兩個正數的算術平均數大于或等于它們的幾何平均數。
2、兩個正數的等差中項大于或等于它們正的等比中項。
探究:如何證明基本不等式√ab≤(a+b)/2(a>0,b>0)?
探究:法2與法3的證明有何不同?如何來使用?
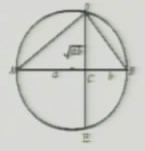
在右圖中,AB是圓的直徑,點C是AB上的一點,AC=a,BC=b,過點C作垂直于AB的弦DE,連接AD、BD,你能利用這個圖形得出基本不等式√ab≤(a+b)/2是幾何解釋嗎?
三、變形不等式與等價關系式
a、變形不等式
已知a,b為正數,證明下列結論
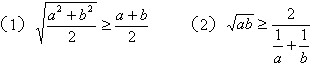
b、3個等價關系式
(1)a2+b2≥2ab ←→ ab≤(a2+b2)/2 (a,b∈R)
(2)√ab≤(a+b)/2 ←→ ab≤[(a+b)/2]2 (a,b∈R+)
(3)√[(a2+b2)/2]≥(a+b)/2 ←→ (a+b)2/2 (a,b∈R+)
其中當且僅當a=b時取等號。
四、基本不等式的簡單應用
例1:證明下列兩個不等式
(1)當a,b∈R+時,a/b+b/a≥2(當且僅當a=b時取“=”號)
(2)當a∈R+時,a+1/a≥2(當且僅當a=1時取“=”號)
例2:已知x,y是正數,求證:
(1)如果積xy是定值p,那么當且僅當x=y時,和x+y有最小值2√p。
(2)如果和x+y是定值s,那么當且僅當x=y時,積xy有最大值(1/4)s2。
課堂思考
某金店有一不準確的天平(臂長不等),顧客要買一串金項鏈,店主分別把項鏈放于左右兩盤各稱一次,然后把兩次稱得質量的算術平均數作為項鏈的質量,問這種稱法是否合理?
此內容正在抓緊時間編輯中,請耐心等待
楊老師
女,中教高級職稱
教學功底扎實,教學經驗豐富,對知識體系有深厚的了解。