課程內容
《簡單的線性規劃問題》
一、提出問題:
若實數x,y滿足不等式組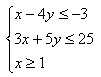
1、上述不等式組表示的平面區域是什么?
2、求z=2x+y的最大值與最小值。
二、有關定義
約束條件、線性約束條件、目標函數、線性目標函數
由x,y的不等式組成的不等式組稱為x,y的約束條件。
欲達到最大值或最小值所涉及的變量x,y的解析式稱為目標函數。
線性規劃:求線性目標函數在線性約束條件下的最大值或最小值的問題,統稱為線性規劃問題。
可行解:滿足線性約束條件的解(x,y)叫可行解。
最優解:使目標函數取得最大或最小值的可行解叫線性規劃問題的最優解。
三、求線性目標函數的最值或取值范圍
原題:求z=2x+y的最大值與最小值(12與3)
變題1:上例若改成求z=x-2y的最大值、最小值呢?
變題2:若改為求z=3x+5y的最大值、最小值呢?
四、實際應用
例4:一個化肥廠生產甲、乙兩種混合肥料,生產1車皮甲種肥料的主要原料是磷酸鹽4t,硝酸鹽18t;生產1車皮乙種肥料需要的主要原料是磷酸鹽1t,硝酸鹽15t。現庫存磷酸鹽10t,硝酸鹽66t。若生產1車皮甲種肥料。產生的利潤為10000元;若生產1車皮乙種肥料,產生的利潤為5000元。在此基礎上,分別生產甲、乙兩種肥料各多少車皮,能夠產生最大的利潤?
思考題:已知:函數f(x)=ax2-c,-4≤f(1)≤-1,-1≤f(2)≤5,求:f(3)的取值范圍。
總結:
解線性規劃問題的一般步驟:
第一步:在平面直角坐標系中作出可行區域;
第二步:在可行區域內找到最優解所對應的點;
第三步:解方程的最優解,從而求出目標函數的最大值或最小值。
解線性規劃應用問題的一般步驟:
(1)理清思路,列出表格;
(2)設好變量x,y,并列出關于x,y的不等式組和目標函數z的解析式;
(3)由二元一次不等式組表示的平面區域作出可行域;
(4)在可行域內求目標函數的最優解;
(5)還原成實際問題(準確作圖,準確計算)。
五、課堂練習
已知x,y滿足不等式組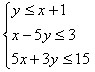
求z=3x+5y的最大值和最小值。
此內容正在抓緊時間編輯中,請耐心等待
楊老師
女,中教高級職稱
教學功底扎實,教學經驗豐富,對知識體系有深厚的了解。