課程內(nèi)容
《二元一次不等式（組）與平面區(qū)域》
一、舉例引出定義
實例：一家銀行的信貸部計劃年初投入25000000元用于企業(yè)和個人貸款，希望這筆資金至少可帶來30000元的收益，其中從企業(yè)貸款中獲益12%，從個人貸款中獲益10%，那么，信貸部應(yīng)該如何分配資金呢？
有關(guān)定義：
（1）二元一次不等式：
含有兩個未知數(shù)，并且未知數(shù)的最高次數(shù)是1的不等式叫做二元一次不等式。
（2）二元一次不等式組：
由幾個二元一次不等式組成的不等式組稱為二元一次不等式組。
（3）二元一次不等式（組）的解集：
滿足二元一次不等式（組）的x和y的取值構(gòu)成有序?qū)崝?shù)對（x，y），所有這樣的有序?qū)崝?shù)對（x，y）構(gòu)成的集合稱為二元一次不等式（組）的解集。
二、二元一次不等式（組）的解集表示的圖形
（1）回憶、思考
回憶：初中一元一次不等式（組）的解集所表示的圖形
（2）二元一次不等式（組）的解集表示什么圖形呢？
先研究具體的二元一次不等式x-y＜6的解集所表示的圖形。
因此，在平面直角坐標系中，不等式x-y＜6表示直線x-y=6左上方的平面區(qū)域，類似的，二元一次不等式x-y＞6表示直線x-y=6右上方的平面區(qū)域。如圖。
直線叫做這兩個區(qū)域的邊界（虛線表示區(qū)域不包括邊界直線）。
通過這個例子推廣到一般情況：
（3）結(jié)論：二元一次不等式Ax+By+C＞0或Ax+By+C＜0在平面直角坐標系中表示直線Ax+By+C=0某一側(cè)所有點組成的平面區(qū)域。（虛線表示區(qū)域不包括邊界）
三、二元一次不等式（組）表示平面區(qū)域的判定方法
方法（1）：取點法（常取坐標原點）
方法（2）：當B＞0時，Ax+By+C＞0表示的點在對應(yīng)直線的上方（左上方或右上方），Ax+By+C＜0表示的點在對應(yīng)直線的下方（左下方或右下方），B＜0則相反，B=0呢？
應(yīng)該注意的幾個問題：
1、應(yīng)準確判斷不等式表示的平面區(qū)域在對應(yīng)直線的哪一側(cè)
2、若不等式中不含0，則邊界應(yīng)畫成虛線，否則應(yīng)畫成實線。
3、畫圖時應(yīng)非常準確，否則將得不到正確結(jié)果。
4、不等式組表示的平面區(qū)域是各個不等式所表示的平面點集，因而是各個不等式所表示的平面區(qū)域的公共部分。
四、應(yīng)用
例1：畫出不等式2x+y-6＜0表示的平面區(qū)域。
例2：畫出不等式組2x+y-2≤0表示的平面區(qū)域。
x-y-2≥0
例3：畫出不等式（x+2y+1）（2x+y-2）＜0表示的平面區(qū)域。
例4：畫出不等式組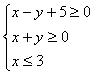
表示的平面區(qū)域。
例5：一個化肥廠生產(chǎn)甲、乙兩種混合肥料，生產(chǎn)1車皮甲種肥料的主要原料是磷酸鹽4t，硝酸鹽18t；生產(chǎn)1車皮乙種肥料需要的主要原料是磷酸鹽1t，硝酸鹽15t。現(xiàn)庫存磷酸鹽10t，硝酸鹽66t，在此基礎(chǔ)上生產(chǎn)這兩種混合肥料。列出滿足生產(chǎn)條件的數(shù)學關(guān)系式，并畫出相應(yīng)的平面區(qū)域。
此內(nèi)容正在抓緊時間編輯中，請耐心等待
楊老師
女，中教高級職稱
教學功底扎實，教學經(jīng)驗豐富，對知識體系有深厚的了解。
