課程內容
《一元二次不等式的解法（2）》
一、復習、回顧
二次函數、一元二次方程、一元二次不等式解集之間的相互關系。
解一元二次不等式的一般步驟：
（1）化不等式為標準式ax2+bx+c＞0或ax2+bx+c＜0（a＞0）
（2）計算△的值，確定方程ax2+bx+c=0的根的情況及求根x1、x2。
（3）根據圖象寫出不等式的解集。
二、含有參數的一元二次不等式的解法
例1：解關于x的不等式x2+5ax+6a2＞0
例2：解關于x的不等式x2-（a+1）x+a＞0
引申：解關于x的不等式ax2+（6a+1）x+6＞0
總結1：對于含參的討論問題要注意：
（1）討論的分界點如何選定
（2）討論要做到不重不漏
三、求參數的值或取值范圍
例3：求函數y=lg（x2-5x-14）的定義域。
引申：若y=lg（x2-5x-14）的定義域為R，求b范圍。
拓展：若y=lg（x2-5x-b）的值域為R，求b范圍。
例4：已知關于x的不等式：（a-2）x2+（a-2）x+1≥0恒成立，試求a的取值范圍。
總結2：含有參數的不等式恒成立的問題（這里指二次不等式恒成立的問題）
（1）二次不等式ax2+bx+c＞0恒成立 ←→ a＞0，△=b2-4ac＜0
（2）二次不等式ax2+bx+c＜0恒成立 ←→ a＜0，△=b2-4ac＜0
（3）二次不等式ax2+bx+c≥0恒成立 ←→ a＞0，△=b2-4ac≤0
（4）二次不等式ax2+bx+c≤0恒成立 ←→ a＜0，△=b2-4ac≤0
四、解告辭不等式和分式不等式
例5：解不等式（x-1）（x2-x-30）＞0
例6：解不等式（2x2-3x-5）/（3x2-13x+4）≥1
五、課堂作業
1、若方程x2+mx+n=0無實數根，則不等式x2+mx+n＞0的解集是________。
2、已知不等式ax2+bx+2＞0的解事-1/2＜x＜1/3，則a=_______，b=_______。
3、若不等式x2+ax+（a+3）＜0的解集是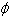
，則實數a的取值范圍是________。
六、課堂小結
1、內容分析：
（1）解含參數的不等式
（2）已知不等式的解集，求參數的值或范圍
（3）不等式中的恒成立為題
（4）會解簡單的高次不等式和分式不等式
2、運用的數學思想：
（1）分類討論的思想
（2）數形結合的思想
（3）等與不等的劃歸思想
此內容正在抓緊時間編輯中，請耐心等待
楊老師
女，中教高級職稱
教學功底扎實，教學經驗豐富，對知識體系有深厚的了解。
